One of the new fellows asked me about a data summary for two groups of patients. The ages were quite different, the mean age was 4.6 years in the exposure group and 8.5 years in the control group. But the control group happened to include a 21 year old patient (a bit of an outlier in a pediatric hospital). In the treatment group, the oldest patient was 10 years old.
To what extent is the outlier influencing the difference in average ages? That's a bit hard to say, but one hint that it was not a major influence was the fact that the medians also showed a large disparity (4.5 for the exposure group versus 7.8 for the control group). The median is not influenced by outliers, so a discrepancy here indicates that the discrepancy in ages would probably persist if you ignored the outlier.
I did not have the original data from this study, but there is a cute trick that allows you to remove a single data point from your summary calculations. It relies on an algorithm for the mean and variance calculations known as the provisional means algorithm. This algorithm updates the mean and variance as each new point in the data set appears. From a computational viewpoint, it is fast because it allows you to compute the mean and variance with a single pass through the data. The alternative algorithms either require two passes through the data or have problems with numerical stability.
Here's the algorithm for updating the mean. The formulas here should appeal to your general intuition.
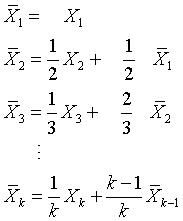
Notice that the average at each step is a weighted sum of the new value and the mean from the previous step. The formula for the variance is a bit less intuitive, but it follows the same general pattern.
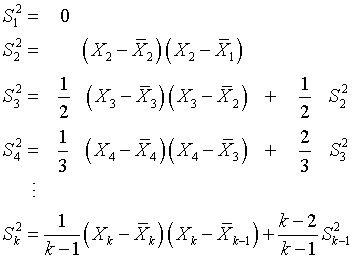
The formulas here are slightly modified from the provisional means algorithm. The actual algorithm uses the sums of squares rather than the variance for the intermediate calculations to save a bit more in computational effort. The standard deviaiton, of course, is just the square root of the variance.
You can run this formula in reverse to remove an individual data point from the summary statistics. Let's look at an example from my standard deviation web page. The data for this example is 73, 58, 67, 93, 33, 18, and 147. You can compute the mean and standard deviation to get 69.9 and 42.2. The variance is 1780.84. How would these numbers change if the last value were removed from the data? Here's the calculation for the mean:
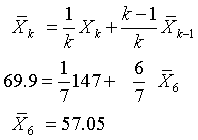
and for the variance and standard deviation:
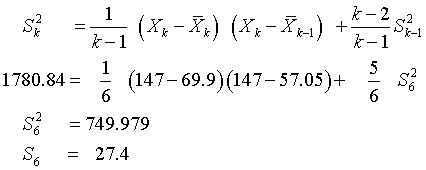
When the largest value is removed from this data set, the mean decrease by about 20% and the standard deviation is reduced by about a third.
Of course, you shouldn't willy-nilly toss out any values just because they look bad. As a general rule, you should not remove outliers unless you have a good medical or scientific reason to do so. Never remove an outlier on the basis of statistics alone.