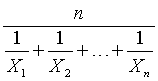
A surprising application of the harmonic mean (February 1, 2005)
This page is moving to a new website.
The radio show, Car Talk, has a puzzle that they read every week on the show. Usually, it is some unusual or unexpected problems with automobiles, but Ray and Tom Magliozzi also will toss in a mathematical puzzle from time to time. A recent car talk puzzler:
discusses a family that has two cars, one which gets 10 miles per gallon and the other gets 100 mpg. Both cars are driven the same number of miles each month. They have the choice of replacing the 100 mpg car with a 200 mpg car or tuning up the 10 mpg car so that it gets 11 mpg. Which strategy, they ask, will lead to the biggest improvement in average gasoline consumption?
The answer may surprise you, though I won't give a detailed answer here. The basic concept, though, is that you need to average the gallons per mile rather than the miles per gallon.
Another way to approach this is to compute the harmonic mean. The formula for the harmonic mean looks unusual:
but you can do the same computation by
The harmonic mean also comes to play in other types of puzzles. For example, you are traveling to a location, and your average speed on the way out is 30 miles per hour. How fast would you have to travel on the return so that the average speed for the entire trip is 60 miles per hour.
A more practical application of the harmonic mean is in calculating the precision of certain estimates when you have unequal sample sizes in each group. For example, suppose you want a confidence interval for the difference between two means. The first group has 25 patients and the second has 100 patients. You can show that the precision of your confidence interval is the same as the precision when both groups have a sample size of 40, the harmonic mean of 25 and 100.
Related pages in Stats:
Further reading