Measuring agreement (April 19, 2005)
This page is moving to a new website.
Someone reviewing a paper asked me about all the "weird statistics" being used in the paper, such as the Bland-Altman plot and Deming regression.
The Bland-Altman plot is a fairly standard way to compare the agreement between two measures of the clinical outcome.
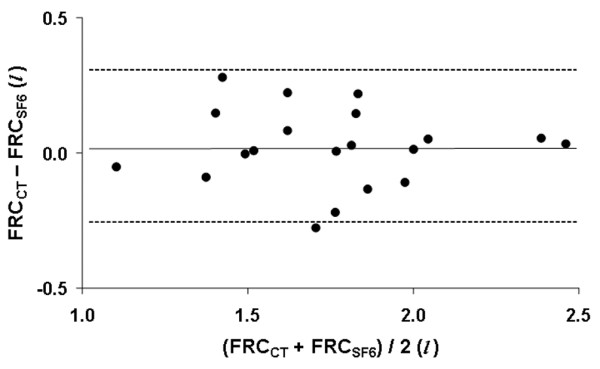
Here's an example of a Bland-Altman plot

that compares functional residual capacity by two approaches: rebreathing of sulphur hexafluoride and by computed tomography. The two measures appear to be reasonably close to one another, and the degree of agreement is about the same across the full range of the data. This graph appears in
which is an open source journal.
Deming regression is just the same thing as linear regression except that an adjustment is made for measurement error in the independent variable.
As an example of Deming regression, two immunoassays for human glandular kallikrein were compared using Deming regression. The slope was 0.79 (95% confidence interval 0.67 to 0.92) and the intercept was 0.014 (95% CI 0.004 to 0.025) with an R-squared value of 0.67. This line (the solid line in the graph below) differs from the ideal line with slope=1 and intercept=0 (the dotted line) and has a weak correlation, since one assay can only account for 2/3 of the variation in the other assay.
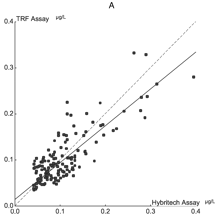
[Permission received on April 25, 2005 to reproduce this image.]
The authors may have also used something called Lin's Concordance Coefficient.
An example of Lin's concordance coefficient appears in a study of joint space narrowing and erosion scores in plain versus digitized x-rays. The erosion concordance score is 0.89 and the graph below shows good agreement between the regression line (solid) and the line of perfect agreement (dashed).

In contrast, the joint space narrowing has a concordance score of only 0.36 and notice how the regression line is not even close to the line of perfect agreement.

These data and figures come from
which is an open source journal.
These tools are little publicized because the measurement of agreement does not fit into the classical statistical models. There is no research hypothesis, for example, but rather the goal of the research is to assess how strongly two measures agree with one another.
Further reading