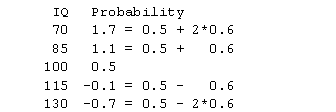
What does a 60% drop mean? (June 20, 2005)
This page is moving to a new website.
A friend sent me an email quoting the following statistic:
"A woman's chances of getting married dropped 60% for every rise of 15 points in her IQ, according to an English study reported in The Atlantic." From 6-05 Touchstone.
I do not have easy access to either The Atlantic or Touchstone magazine. But the number seemed too large to be credible. so I ran a few simple calculations. First, I assumed that the probability of marriage was 50% for women with an average IQ (100 points). This value is probably quite a bit low, but serves as a basis for easy computation.
So what does a 60% drop mean. Your first thought might be to subtract 60% for each 15 points in IQ. This doesn't make sense, though for any simple calculations. Subtracting 60% means that the probability of marriage would be -10% for a woman with an IQ of 115 and -70% for a woman with an IQ of 130. Going in the opposite direction makes things even worse. A woman with an IQ of 85 would have a 110% chance of marriage and a woman with an IQ of 70 would have a 170% chance of getting married.
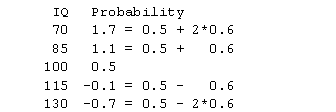
So you know right away that the probability is not additive. Maybe it is a relative probability, which means that you multiply rather than add. Let's see how that works.
A 60% drop means that the probability decreases to 40% of the original value if the IQ increases by 15 points. Let's start again with the probability being 0.5 for a woman with an average IQ. Then a woman with an IQ of 115 would have a probability of only 20% and a woman with an IQ of 130 would have a probability of only 8%. These numbers seem too extreme to me, but it gets even worse when you look at below average IQs. To find the probability of marriage for a woman of IQ 85, you would divide 50% by 40%. This creates a probability of 125%. For a woman with an IQ of 70, the probability would be 312%, clearly an impossible value unless polygamy is allowed.
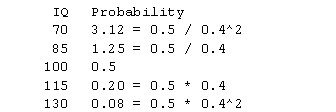
What the 60% probably refers to is a 60% change in the odds of getting married. This corresponds to an odds ratio of 0.4. It may help to compute the reciprocal odds ratio 2.5 (=1/0.4). This tells you that the odds of marriage decrease 2.5 times for every 15 unit increase in IQ and increase 2.5 times for every 15 unit decrease in IQ. A 30 unit shift would produce a 6.25 (=2.5^2) change in the odds of marriage. Here are the calculations.

Converting from odds to probability is a bit tricky. The formula depends on whether the odds are in favor of the event or against the event.
So four to one odds in favor of an event translates into 4/5 or an 80% probability. Four to one odds against an event translates into 1/5 or a 20% probability.
These numbers still look to extreme to me. So I decided to try to hunt down the original article. The closest thing I could find was
Childhood IQ and marriage by mid-life: the Scottish Mental Survey 1932 and the Midspan studies. Personality and Individual Differences, Vol. In Press, Corrected Proof. Taylor MD, Hart CL, Smith GD, Whalley LJ, Hole DJ, Wilson V, Deary IJ.
which was mentioned on a website called CiteULike. The address for this particular article is
I could not find this paper anywhere else, such as on PubMed. The abstract has the following sentence:
Among women, the odds ratio of ever marrying by mid-life was 0.42 (95% CI 0.27-0.64; p = 0.0001) for each standard deviation increase in childhood IQ.
So my hunch about the 60% drop being a change in odds was right.
I'll try to look into this further. I suspect there are some serious limitations to this study because probabilities seem too extreme to be plausible. These probabilities range from 14% for women with IQs that place them among the professional class (130 points) to 71% for women with IQs that probably place them in the borderline employable category (85 points). Does anyone truly believe that there is this degree of disparity in marriage rates?
It may be like the infamous statistic that a 35 year old never married woman was more likely to be killed by a terrorist than get married. As I recall, that statistic got a lot of press before it was debunked. I can't find good details on this statistic either, so anyone who reads this and knows of a good source, please let me know.
Joel Best has a nice book on how statistics can get mangled.