Confidence intervals around a safety level (created 2005-05-11).
This page is moving to a new website.
Someone asked me about an environmental clean up. The government told them that the location was cleaned up to a 90% confidence level of the standard. Would this give the residents an assurance that everything was safe?
I don't have the background to answer all of this question, but can comment on the Statistical aspects.
The government has set a standard that represents a safe level of exposure. How that standard is set is always controversial and some people will argue that it should be higher and some will argue that it should be lower. Let's assume that the standard that they set is reasonable, because I would not be able to tell you whether it is or it isn't.
Let me make up a number, 500, and pretend that anything less than that represents a safe level of exposure. Where the Statistics will come into play is with the 90% confidence level.
There are some limitations in how you sample exposure levels. You can't sample all times and all locations, because it would cost too much and/or would take too long to get an answer. So the government tells you, in acknowledgement of the fact that they can't do a completely comprehensive study (no one could be perfectly comprehensive, to be honest), they will make sure that the levels are lower than the safe level.
How much lower? Low enough so that even after allowing for sampling error, there is still evidence that the levels are safe. So a measurement of 450+/-50 would work, or 300+/-200, or 100+/-400 or even 495+/-5. If that's the way they did it, it actually works to your advantage. They wouldn't want to do a haphazard job of sampling, because then the margin of sampling error would be so large that they could never get the plant clean enough. The confidence interval of 100+/-400 might represent such a scenario. So they have a financial incentive to make sure that the sampling that they do is thorough and complete. But of course, they would not want to make the sampling overly ornate. If their interval were 495 +/-5, they would be spending too much money on the sampling, and maybe they should have spent some of that money doing a bit of extra clean up.
Here's a numeric example to illustrate the problem. Let's suppose that the current level of the environmental site is at 600, a dangerous level. Let's also suppose that it costs $10,000 to reduce the level by one unit. If there were no issues with sampling error, then the cost of the clean-up would be one million dollars (100 units of reduction times 10 thousand dollars per unit).
But the sampling to indicate how much we have reduced the level is both imperfect and expensive. It costs $5,000 per site to sample and the standard deviation for any individual site measurement would be 200 units. You can use the spreadsheet
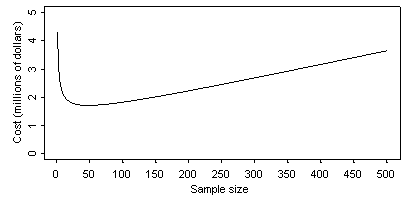
to calculate 90% confidence intervals. Let's suppose first that we wanted to do a minimal job of sampling and only selected 8 sites to sample. We would get 90% confidence limits of +/-134. That means that we would have to spend an extra 1.34 million dollars to get the remediation needed so that our upper confidence limit was still in the safe range. But at least the sampling wouldn't cost so much. We would have only spent 40 thousand dollars on the sampling. Total bill: 2.38 million dollars.
With a sample of 100 sites, the confidence interval would be +/- 33. The cost of the extra remediation is now only $330,000, but the cost of the sampling has jumped up to $500,000. Total bill: 1.83 million dollars.
With a sample of 500 sites, the confidence interval would be +/- 15. So there would only be $150,000 in extra remediation costs. But the cost of the sampling has gone through the roof. We're now paying $2,500,000 just for the sampling. Total bill: 3.65 million.
Here's a graph of all possible sample sizes and total costs.

It turns out that the most economical sample size is 50. It leads a confidence interval of +/-47 and a total bill of 1.72 million dollars.
Now, why did the government use a 90% interval rather than a 95% interval? It turns out that when you are interested in errors only in one direction (no one is unhappy if the plant is cleaner than you estimate it to be), then a 90% interval makes more sense. The EPA did this with their report on passive smoking. They wanted to see if there was evidence that passive smoking caused lung cancer. They use a 90% confidence interval because no one treated seriously the possibility that passive smoking was protective against lung cancer. Well almost no one. The tobacco companies found a judge in North Carolina who told the EPA that a 90% confidence level violated the scientific norms and tossed out their report.
This is a bit of a digression, but what is the bottom line? I cannot comment on whether 500 is a safe level or if it should be higher or lower. The only thing I know for sure is that zero is an unreasonable value.
I can comment on the confidence intervals, though. If the government set up the confidence intervals in a way so that they were forced to err on the safe side if the sampling plan was inadequate, then you have a good deal of protection, because it then forces them to use a thorough rather than a haphazard sampling plan.
This page was written by Steve Simon while working at Children's Mercy Hospital. Although I do not hold the copyright for this material, I am reproducing it here as a service, as it is no longer available on the Children's Mercy Hospital website. Need more information? I have a page with general help resources. You can also browse for pages similar to this one at Category: Confidence intervals.