[The Monthly Mean] July/August 2009--You, too, can understand Bayesian data analysis (released 2009-09-11)

Monthly Mean newsletter, July/August 2009

The monthly mean for July/August is 16. Please note that no other mean across two consecutive months, except December/January, is as large. I had believed the story that Caesar Augustus had swiped a day from February and added it to August so "his" month would not be shorter than Julius Caesar's month (July). Unfortunately, like most good stories, this one is false. See en.wikipedia.org/wiki/Julian_calendar#Debunked_theory_on_month_lengths.

Welcome to the Monthly Mean newsletter for July/August 2009. This newsletter was sent out on September 11, 2009. If you are having trouble reading this newsletter in your email system, please go to www.pmean.com/news/2009-08.html. If you are not yet subscribed to this newsletter, you can sign on at www.pmean.com/news. If you no longer wish to receive this newsletter, there is a link to unsubscribe at the bottom of this email. Here's a list of topics.
Lead article: You, too, can understand Bayesian data analysis
2. Risk adjustment using reweighting
3. The second deadly sin of researchers: sloth
4. Monthly Mean Article (peer reviewed): Comparison of Registered and Published Primary Outcomes in Randomized Controlled Trials.
5. Monthly Mean Article (popular press): For Today's Graduate, Just One Word: Statistics
6. Monthly Mean Book: Understanding Variation
7. Monthly Mean Definition: Weighted mean
8. Monthly Mean Quote: Wall Street indexes predicted ...
9. Monthly Mean Website: Spreadsheet Addiction
10. Nick News: Nicholas the fishmonger
11. Very bad joke: A statistician is someone who enjoys working with numbers, but...
12. Tell me what you think.
13. Free statistics webinar: Wednesday, October 14, 2009, 10am-noon CDT.

1. Lead article: You, too, can understand Bayesian data analysis

Bayesian data analysis seems hard, and it is. Even for me, I struggle with understanding Bayesian data analysis. In fairness, I must admit that much of my discomfort is just lack of experience with Bayesian methods. In fact, I've found that in some ways, Bayesian data analysis is simpler than classical data analysis. You, too, can understand Bayesian data analysis, even if you'll never be an expert at it. There's a wonderful example of Bayesian data analysis at work that is simple and fun. It's taken directly from an article by Jim Albert in the Journal of Statistics Education (1995, vol. 3 no. 3) which is available on the web at www.amstat.org/publications/jse/v3n3/albert.html.

I want to use his second example, involving a comparison of ECMO to conventional therapy in the treatment of babies with severe respiratory failure. In this study, 28 of 29 babies assigned to ECMO survived and 6 of 10 babies assigned to conventional therapy survived. Refer to the Albert article for the source of the original data. Before I show how Jim Albert tackled a Bayesian analysis of this data, let me review the general paradigm of Bayesian data analysis.

Wikipedia gives a nice general introduction to the concept of Bayesian data analysis with the following formula:

P (H|E) = P(E|H) P(H) / P(E)

where H represents a particular hypothesis, and E represents evidence (data). P, of course, stands for probability. I don't like to present a lot of formulas in this newsletter, but this one is not too complicated. If you follow this formula carefully, you will see there are four steps in a typical Bayesian analysis.

The first step is to specify P(H), which is called the prior probability. Specifying the prior probability is probably the one aspect of Bayesian data analysis that causes the most controversy. The prior probability represents the degree of belief that you have in a particular hypothesis prior to collection of your data. The prior distribution can incorporate data from previous related studies or it can incorporate subjective impressions of the researcher. What!?! you're saying right now. Aren't statistics supposed to remove the need for subjective opinions? There is a lot that can be written about this, but I would just like to note a few things.

First, it is impossible to totally remove subjective opinion from a data analysis. You can't do research without adopting some informal rules. These rules may be reasonable, they may be supported to some extent by empirical data, but they are still applied in a largely subjective fashion. Here are some of the subjective beliefs that I use in my work:

you should always prefer a simple model to a complex model if both predict the data with the same level of precision.

you should be cautious about any subgroup finding that was not pre-specified in the research protocol.

if you can find a plausible biological mechanism, that adds credibility to your results.

Advocates of Bayesian data analysis will point out that use of prior distributions will force you to explicit some of the subjective opinions that you bring with you to the data analysis.

Second, the use of a range of prior distributions can help resolve controversies involving conflicting beliefs. For example, an important research question is whether a research finding should "close the book" to further research. If data indicates a negative result, and this result is negative even using an optimistic prior probability, then all researchers, even those with the most optimistic hopes for the therapy, should move on. Similarly, if the data indicates a positive result, and this result is positive even using a pessimistic prior probability, then it's time for everyone to adopt the new therapy. Now, you shouldn't let the research agenda be held hostage by extremely optimistic or pessimistic priors, but if any reasonable prior indicates the same final result, then any reasonable person should close the book on this research area.

Third, while Bayesian data analysis allows you to incorporate subjective opinions into your prior probability, it does not require you to incorporate subjectivity. Many Bayesian data analyses use what it called a diffuse or non-informative prior distribution. This is a prior distribution that is neither optimistic nor pessimistic, but spreads the probability more or less evenly across all hypotheses.

Here's a simple example of a diffuse prior that Dr. Albert used for the ECMO versus conventional therapy example. Let's assume that the true survival rate could be either 0, 10%, 20%, ..., 100% in the ECMO group and similarly for the conventional therapy group. This is not an optimal assumption, but it isn't terrible either, and it allows us to see some of the calculations in action. With 11 probabilities for ECMO and 11 probabilities for conventional therapy, we have 121 possible combinations. How should we arrange those probabilities? One possibility is to assign half of the total probability to combinations where the probabilities are the same for ECMO and conventional therapy and the remaining half to combinations where the probabilities are different. Split each of these probabilities evenly over all the combinations.

If you split 0.50 among the eleven combinations where the two survival rates are equal, you get 0.04545. Splitting 0.50 among the 110 combinations where the two survival rates are unequal, you get 0.004545.

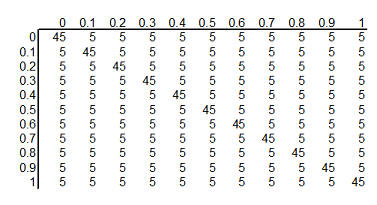
You can arrange these prior probabilities into a rectangular grid where the columns represent a specific survival rate with ECMO and the rows represent a specific survival rate with conventional therapy. To simplify the display, we multiplied each probability by 1000 and rounded the result. So we have 121 hypotheses, ranging from ECMO and conventional therapy both having 0% survival rates to ECMO having 100% survival and conventional therapy having 0% survival rates to ECMO having 0% and conventional therapy having 100% survival rates to both therapies having 100% surivival rates. Each hypothesis has a probability assigned to it. The probability for ECMO 90% and conventional therapy 60% has a probability of roughly 5 in a thousand and the probability for ECMO 80% and conventional therapy 80% has a probability of roughly 45 in a thousand.

The second step in a Bayesian data analysis is to calculate P(E | H), the probability of the observed data under each hypothesis. If the ECMO survival rate is 90% and the conventional therapy survival rate is 60%, then the probability of observed 28 out of 29 survivors in the ECMO group is 152 out of one thousand, the probability of observing 6 out of 10 survivors in the conventional therapy group is 251 out of one thousand. The product of those two probabilities is 38,152 out of one million which we can round to 38 out of one thousand. If you've forgotten how to calculate probabilities like this, that's okay. It involves the binomial distribution, and there are functions in many programs that will produce this calculation for you. In Microsoft Excel, for example, you can use the following formula.

binomdist(28,29,0.9,FALSE)*binomdist(6,10,0.6,FALSE)

The calculation under different hypotheses will lead to different probabilities. If both ECMO and conventional therapy have a survival probability of 0.8, Then the probability of 28 out of 29 for ECMO is 11 out of one thousand, the probability of 6 out of 10 for conventional therapy is 88 out of one thousand. The product of these two probabilities is 968 out of one million, which we round to 1 out of one thousand.

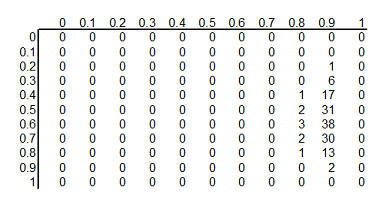
The table above shows the binomial probabilities under each of the 121 different hypotheses. Many of the probabilities are much smaller than one out of one thousand. The likelihood of seeing 28 survivals out of 29 babies in the ECMO survivals is very small when the hypothesized survival rate is 10%, 30%, or even 50%. Very small probabilities are represented by zeros.

Now multiply the prior probability of each hypothesis by the likelihood of the data under each hypothesis. For ECMO=0.9, conventional therapy=0.6, this product is 5 out of a thousand times 38 out of a thousand, which equals 190 out of a million (actually it is 173 out of a million when you don't round the data so much). For ECMO=conventional=0.8, the product is 45 out of a thousand times 1 out of a thousand, or 45 out of a million.

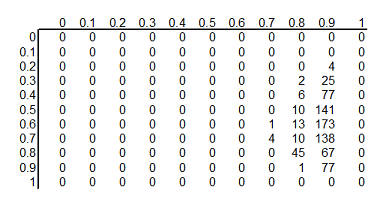
This table shows the product of the prior probabilities and the likelihoods. We're almost done, but there is one catch. These numbers do not add up to 1 (they add up to 794 out of a million), so we need to rescale them. We divide by P(E) which is defined in the wikipedia article as

P(E) = P(E|H1) P(H1) + P(E|H2) P(H2) + ...

In the example shown here, this calculation is pretty easy: add up the 121 cells to get 794 out of a million and then divide each cell by that sum. For more complex setting, this calculation requires some calculus, which should put some fear and dread into most of you. It turns out that even experts in Calculus will find it impossible to get an answer for some data analysis settings, so often Bayesian data analysis requires computer simulations at this point.

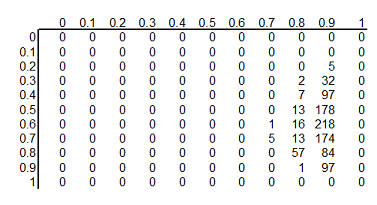
Here's the table after standardizing all the terms so they add up to 1.

This table is the posterior probabilities, P(H | E). You can combine and manipulate these posterior probabilities far more easily than classical statistics would allow. For example, how likely are we to believe the hypothesis that ECMO and conventional therapy have the same survival rates? Just add the cells along the diagonal (0+0+...+5+57+97+0) to get 159 out of a thousand. Prior to collecting the data, we placed the probability that the two rates were equal at 500 out of a thousand, so the data has greatly (but not completely) dissuaded us from this belief. You can calculate the probability that ECMO is exactly 10% better than conventional therapy (0+0+...+1+13+84+0 = 98 out of a thousand), that ECMO is exactly 20% better (0+0+...+13+218+0 = 231 out of a thousand), exactly 30% better (0+0+...+7+178+0 = 185 out of a thousand), and so forth.

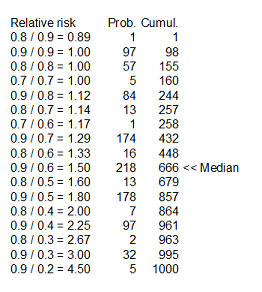
Here's something fun that Dr. Albert didn't show. You could take each of the cells in the table, compute a ratio of survival rates and then calculate the median of these ratios as 1.5 (see above for details). You might argue that 1.33 is a "better" median because 448 is closer to 500 than 666, and I wouldn't argue too much with you about that choice.

Dr. Albert goes on to show an informative prior distribution. There is a fair amount of data to indicate that the survival rate for the conventional therapy is somewhere between 10% and 30%, but little or no data about the survival rates under ECMO.

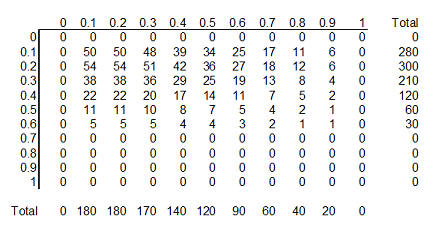
The table above shows this informative prior distribution. Recall that the rows represent survival rates under conventional therapy. This prior distribution restricts the probabilities for survival rates in the conventional therapy to less than 70%. There is no such absolute restriction for ECMO, though the probabilities for survival rates of 70% and higher are fairly small.

In future newsletters, I'd like to show other simple examples of Bayesian data analysis.

2. Risk adjustment using reweighting

In the May/June newsletter, I introduced a dataset on average salaries at colleges/universities in each of the 50 states plus the District of Columbia. Each state had a different mix of Division I, IIA, and IIB colleges/universities and this could potentially distort the statewide average. I then showed how covariate adjustment could be used to produce estimates that removed this effect from the calculation.

This month, I'd like to show a different approach, reweighting, that can adjust for the variations in proportions of I, IIA, and IIB in a particular state. West Virginia is an interesting state because it has one of the lowest average faculty salaries, averaged across all of its colleges/universities, but it also has a disproportionate share of Division IIB colleges. The average salary is $45 thousand among the Division I schools which represent 6% of the WV schools. The average salary is $40 thousand among the Division IIA schools, which also represents 6% of the total. The remainder of the schools (88%) are Division IIB schools with a much lower average salary ($34 thousand).

You can compute the overall salary for WV by multiplying the individual averages by their respective proportions. The overall average salary in WV is $35.1 which is computed as 0.06*45 + 0.06*40 + 0.88*34.

The graph shown above demonstrates how the large number of IIB schools drags down the overall average.

What would happen if you could transform WV to a state that had the same proportion of I, IIA, and IIB schools as the overall proportions in the United States (16%, 32%, and 53%, respectively). The calculation using different weights would be 0.16*45 + 0.32*40 + 0.53*34 which equals $38 thousand. This adjusted estimate shows that almost $3 thousand in the relatively low WV overall average can be accounted for by the disproportionately large number of IIB schools in the state.

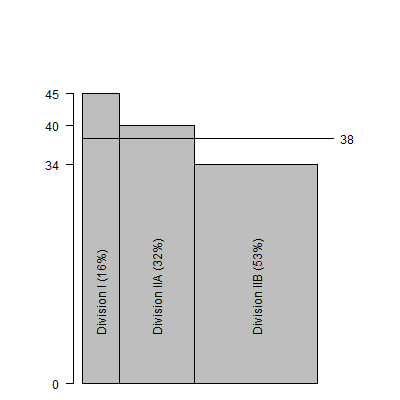
The graph shown above demonstrates how the higher adjusted average would be computed by shrinking the IIB bar and expanding the I and IIA bars to reflect proportions observed across the entire US.

The salaries observed in the District of Columbia exhibit a different problem. In DC, the average salary across all Division I schools is $57 thousand. These schools account for a disproportionately large proportion of DC schools (56% versus 16%). The average salaries across all Division IIA and IIB schools are $50 thousand and $33 thousand respectively, and the proportions of these schools (22% and 22%) are both below the nationwide proportions. If you computed a simple average across all the schools is would be 0.56*57 + 0.22*50 +0.22*33.

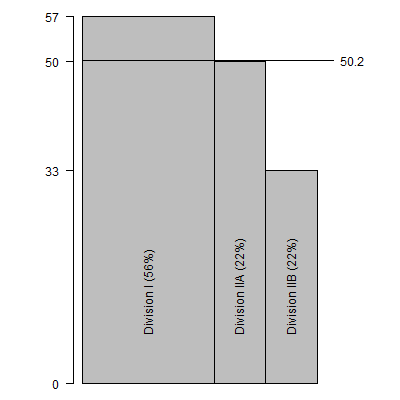
The above graph shows this calculation, which produces an overall average of $50.2 thousand, an average higher than most states. But how much of this is because of the relatively large proportion of Division I schools?

If you change the weights and recalculate the average would be 0.16*57 + 0.32*50 + 0.53*33.

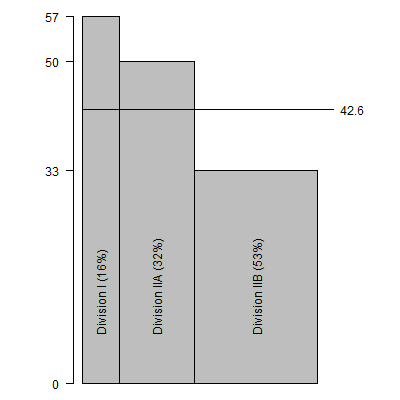
This figure illustrates the recalculation with a much narrower bar for Division I and wider bars for Division IIA and IIB. The adjusted estimate is $42.6 thousand. Thus $7.6 thousand dollars of the average DC salary is accounted for by the disproportionately large number of Division I schools.

There are still other approaches to risk adjustment, such as the case mix index and propensity scores, that I will discuss in future newsletters. This work was part of a project I am helping with: the adjustment of outcome measures in the National Database of Nursing Quality Indicators. The work described in this article was supported in part through a grant of the American Nursing Association.

3. The second deadly sin of researchers: sloth

In the last newsletter, I mentioned the first deadly sin of researchers, pride. Researchers are too proud to use an existing survey/scale and want to develop one of their own. They know things better than anyone else. Unfortunately, the proliferation of surveys/scales leads to a fragmented body of research.

The second deadly sin of researchers is sloth. Researchers often take the easy way out. Again, the evidence for this comes from a large scale review by Ben Thornley and Clive Adams of research on schizophrenia. You can find the full text of this article on the web at bmj.com/cgi/content/full/317/7167/1181. Thornley and Adams noted that the vast majority of studies were conducted in an inpatient setting. Inpatients are easier to study because you just walk down the hallway to collect data. But community based studies which are harder to conduct, are used in only 14% of the studies, though this proportion did increase somewhat over time.

This sort of thing occurs too often in psychology studies, where tests are conducted on college age volunteers. Given that most Psychology researchers work at colleges and universities, it is clearly easy to recruit college age students, but it is unclear whether results from the group will extrapolate well to other segments of society.

Thornley and Adams also suggested that a good study of schizophrenia should last at least six MONTHS, but most studies (54%) lasted six WEEKS or less. In general, short term outcomes require less effort, but the clinical relevance of those outcomes is questionable. In a weight loss study, just about any diet, exercise, or other intervention will get people to lose weight for a few weeks or a month. The true value of the intervention, though, is in whether that intervention can maintain that weight loss over a span of one or more years.

Finally, Thornley and Adams suggested that a total sample size of 300 would be needed to have reasonable power and precision, but the average study had just 65 total participants. Only 3% of the studies met or exceeded a total sample size of 300. This last point has also been emphasized by other researchers. The typical research study is too small and provides too little power and precision. But researchers are too lazy to take the effort to collect an appropriate sample size, as it would require too much time. You can increase sample size by considering mutli-center trials, but this is also too much effort for most researchers.

Too many researchers take the easy way out, by studying the easy-to-study patients, studying them for too short a period of time, and recruiting far too few patients. There is some value in starting with the easy research, picking the low-hanging fruit. Still the general research opus is skewed too heavily in this direction. Not enough of the research makes the leap to the more difficult to recruit but more relevant population. Not enough research examines long term outcomes. Not enough research collects an adequate sample size.

4. Monthly Mean Article (peer-reviewed): Comparison of Registered and Published Primary Outcomes in Randomized Controlled Trials.

Mathieu S, Boutron I, Moher D, Altman DG, Ravaud P. Comparison of Registered and Published Primary Outcomes in Randomized Controlled Trials. JAMA. 2009;302(9):977-984. Comment: Only the abstract is freely available today (September 3, 2009), but if the full article is consistent with the abstract, this is a very shocking finding. Most registered trials are ambiguous about the primary outcome measure. The ones that are not ambiguous frequently show a major discrepancy between the primary outcome as reported in the publication versus the primary outcome specified in the registry. Available at: jama.ama-assn.org/cgi/content/abstract/302/9/977 [Accessed September 3, 2009].

5. Monthly Mean Article (popular press): For Today's Graduate, Just One Word: Statistics

Lohr, Steve (2009, August 5). For Today's Graduate, Just One Word: Statistics. The New York Times, August 5, 2009. Available at www.nytimes.com/2009/08/06/technology/06stats.html. This article gives a somewhat narrow interpretation of statistics as data mining on web data. It does show how important Google views Statistics in their efforts to optimize their search engine, and you have to love an article with the quote "The rising stature of statisticians, who can earn $125,000 at top companies in their first year after getting a doctorate, is a byproduct of the recent explosion of digital data." I think I'm going to have to raise my consulting rates.

6. Monthly Mean Book: Understanding Variation

Wheeler, Donald (2000). Understanding Variation: The Kay to Managing Chaos, SPC Press, Knoxville, TN. ISBN: 0945320531. I've recommended this book to people more than any other book in my collection. It gives you a good understanding of how and why you want to use control charts to improve quality at your workplace. It's written at a level that anyone can understand, no matter how little mathematics background you have.

7. Monthly Mean Definition: Weighted mean

The weighted mean is a mean where the relative contribution of individual data values to the mean is not the same. Each data value (X_i) has a weight assigned to it (W_i). Data values with larger weights contribute more to the weighted mean and data values with smaller weights contribute less to the weighted mean. In the simpler unweighted mean, each data value is added together and the sum is divided by the number of values in the sample. A formula for the weighted mean would be

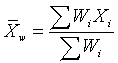
If the weights are computed so that their sum is 1, then the formula shown above can dispense with the denominator.

There are several reasons why you might want to use a weighted mean.

Each data value might actually represent a value that is used by multiple people in your sample. The weight, then, is the number of people associated with that particular value.

Your sample might deliberately over represent or under represent certain segments of the population. Some of the nationwide surveys produced by the Centers for Disease Control and Prevention deliberately oversample African-American and Hispanic groups so that there would be sufficient precision to track statistics in these minority groups. To restore balance, you would place less weight on the over represented segments of the population and greater weight on the under represented segments of the population.

Some values in your data sample might be known to be less variable (more precise) than other values. You would place greater weight on those data values known to have greater precision.

This definition originally appeared in my old website at: www.childrensmercy.org/stats/definitions/weightedmean.htm.

8. Monthly Mean Quote: Wall Street indexes predicted ...

To prove that Wall Street is an early omen of movements still to come in GNP, commentators quote economic studies alleging that market downturns predicted four out of the last five recessions. That is an understatement. Wall Street indexes predicted nine out of the last five recessions! And its mistakes were beauties. -- Paul Samuelson, "Science and Stocks," Newsweek, September 1966, as cited in www.barrypopik.com/index.php/new_york_city/entry/wall_street_indexes_predicted_nine_out_of_the_last_five_recessions/

9. Monthly Mean Website: Spreadsheet Addiction

Burns P. Spreadsheet Addiction. Available at: www.burns-stat.com/pages/Tutor/spreadsheet_addiction.html [Accessed August 18, 2009]. Excerpt: The goal of computing is not to get an answer, but to get the correct answer. Often a wrong answer is much worse than no answer at all. There are a number of features of spreadsheets that present a challenge to error-free computing.

10. Nick News: Nicholas the fishmonger

Nicholas bought a blue betta on Saturday. It's the first pet that is "his" and not Mom's or Dad's. Here's a picture.

Find out the name we chose at http://www.pmean.com/personal/fishmonger.html.

11. Very bad joke: A statistician is someone who enjoys work with numbers, but...

...doesn't have enough personality to be an accountant.

This is one of my favorite jokes to tell and it always gets a laugh. I don't believe this joke, by the way, but a little bit of self deprecatory humor goes a long way. Various versions of this joke are around on the Internet, and sometimes economist or actuary is substituted for statistician. Go to www.math.utah.edu/~cherk/mathjokes.html for an example.

12. Tell me what you think.

How did you like this newsletter? I have six short questions that I'd like to ask. It's totally optional on your part. Your responses will be kept anonymous, and will only be used to help improve future versions of this newsletter.

Only two people sent feedback (that's okay, I know that you all love my newsletter). I got compliments on my description of mosaic plots. I also got compliments on the material on covariate adjustment from one person, but another person found that material confusing.

Suggestions of future topics included meta-analysis statistics, Bayesian statistics, various methods for smoothing and checking for interactions with applications to survival analysis, and the problem with ROC curves. That's quite an ambitious list.

13. Free statistics webinar: Wednesday, October 14, 2009, 10am-noon CDT.

I want to offer statistics webinars (web seminars) on a variety of topics. A possible list of topics appears at http://www.pmean.com/09/TentativeTraining.html.

To get the ball rolling, I am offering the first webinar for free. This is not free to me, of course, as there are substantial expenses associated with the production of a webinar. In exchange for the free seminar, I'm asking you to send me some suggestions about future statistics webinar topics prior to the webinar and to offer constructive criticism of my first webinar afterwards.

The topic of my first statistics webinar is "What do all these numbers mean? P-values and confidence intervals and the Bayesian alternatives." I don't have the vendor selected yet, but I am looking at Webex and Vcall.

If the free webinar is successful, I plan to hold additional webinars for a reasonable fee, one per month. If you are interested in attending the October webinar or future webinars, please respond to this email or send an email to mail (at) pmean (dot) com with the words "Statistics webinar" in the title. I'll send out another reminder in early October, hopefully along with the September issue of The Monthly Mean.

What now?

Sign up for the Monthly Mean newsletter

Review the archive of Monthly Mean newsletters

Go to the main page of the P.Mean website

Get help

This work is licensed under a Creative Commons Attribution 3.0 United States License. This page was written by Steve Simon and was last modified on 2017-06-15. Need more information? I have a page with general help resources. You can also browse for pages similar to this one at Category: Website details.