[Previous issue] [Next issue]
[The Monthly Mean] July 2010--My sample size is too small, but that's okay
because it is a pilot study
The Monthly Mean is a newsletter with articles about Statistics with
occasional forays into research ethics and evidence based medicine. I try to
keep the articles non-technical, as far as that is possible in Statistics. The
newsletter also includes links to interesting articles and websites. There is
a very bad joke in every newsletter as well as a bit of personal news about me
and my family. If you are not yet subscribed to this newsletter, you can sign
on at
www.pmean.com/news.
Welcome to the Monthly Mean newsletter for July 2010. If you are having
trouble reading this newsletter in your email system, please go to
www.pmean.com/news/201007.html. If you are not yet subscribed to this
newsletter, you can sign on at
www.pmean.com/news. If you no longer wish to receive this newsletter, there is a link to unsubscribe at the bottom
of this email. Here's a list of topics.
Lead article: My sample size is too small, but that's okay
because it is a pilot study
2. Reading SPSS output for a two-sample t-test
3. The rule of three
4. Monthly Mean Article (peer reviewed): When Intuition And Math
Probably Look Wrong
5. Monthly Mean Article (popular press): Numberplay: Your Money
or Your Logic
6. Monthly Mean Book: Health measurement scales
7. Monthly Mean Definition: What is a fishbone diagram?
8. Monthly Mean Quote: The government is extremely fond...
9. Monthly Mean Unsung Hero Award: Ed Rigdon
10. Monthly Mean Website: Research Papers on Inter-Rater
Reliability Estimation
11. Nick News: Nicholas carries a big chunk of the Mendenhall
glacier
12. Very bad joke: How many statisticians...
13. Tell me what you think.
14. Upcoming statistics webinars
15. Join me on Facebook and LinkedIn
1. My sample size is too small, but that's okay because it
is a pilot study
A common dodge that researchers will use when they know their sample size is
too small is to say, that's okay, it's just a pilot study. I discourage this
with anyone I consult with, because a pilot study is not a miniature clinical
trial. The pilot study serves a different goal and it brings with it some extra
requirements that are not needed for a regular clinical trial.
A pilot study exists not for its own benefit, but for the planning of a
larger study to be conducted sometime in the future. That larger study doesn't
need to be conducted by you, but you need to explain what you expect that larger
study to look like and to justify how your pilot study will help in the design
of that larger study.
Pilot studies can provide the following information for planning purposes.
* Estimation of the standard deviation of your outcome measure. The
variability of your outcome measure is a critical component in many sample size
justification approaches such as power calculations. According to one source,
you should get at least 30 observations to insure that your standard deviation
is reasonably stable, but that you should also use not the standard deviation,
but the 80% upper confidence limit for the standard deviation in any sample size
justifications.
* Participation rates. Not everyone you approach will qualify for your
study and some who do qualify may refuse to participate. A pilot study can help
you estimate the proportions of exclusions and refusals among potential
participants so you can estimate a reasonable time frame for completion of a
larger study. You can also use a pilot to estimate dropout rates and
non-compliance rates.
* Resource requirements. Do you have enough space, enough people, and
enough money for the larger study? Estimating resource requirements on a small
scale in a pilot will help you budget money and resources appropriately for the
larger study.
These are quantitative data that you can get from a pilot data. You can also
get qualitative data. Most of this type of data involves trying to avoid
"Murphy's Law" (anything that can go wrong will go wrong). You'd
rather have something go wrong during the small and inexpensive pilot rather
than see it ruin the large and expensive study that you are planning.
It's impossible to list all ways that a study
could go wrong, but here are some areas that you should focus on.
Recruitment and retention problems.
In addition to direct estimates of exclusion and refusal rates, you can look
generally at the type of patients who get into the study.
* Do you get the types of subjects that you
think you will get?
* Are important segments of your population
being left out?Ambiguous situations.
* Is it obvious who meets and who does not
meet the eligibility requirements?
* Do your subjects provide no answer,
multiple answers, qualified answers, or unanticipated answers to your
survey?Time and resource problems
* Does it take too long for your subjects to
fill out all the survey forms?
* Will the study participants overload your
phone lines or overflow your waiting room?
* How much time does it take to mail out a
thousand surveys, and can your tongue lick that many stamps in one day?Machinery problems.
* Is the equipment readily available when and
where you need it?
* What happens when it breaks down or gets
stolen?
* If the machine produces a stream of electronic data, can your computer
software read and understand this data?Data management problems.
* Is there enough room on the data collection
form for all of the data you receive?
* Do you have any problems entering your data
into the computer?
* Can you match data that comes in from
different sources?
* Were any important data values forgotten
about?
* Does your data show too much or too little variability?Uninformative data
* Are most of your lab results are below the
limit of detection?
* Does everybody gives the identical answer
to a survey question?If your study doesn't directly address any of the goals listed above it's
probably not a pilot study.
I talk more about pilot studies on my website:
*
www.pmean.com/04/PilotStudy.html
* www.pmean.com/99/pilot.html
2. Reading SPSS output for a two-sample t-test
One of the skills that comes only with practice is the ability to look at the
output from a program like SPSS and pick out the important numbers. This is
especially tricky when you are running a two-sample t-test, as SPSS
provides more information than you really need. Here's a quick look at what you
should focus on.
The following example involves a data set of 117 houses in Albuquerque, New
Mexico, in 1994. One of the interesting questions is whether the average sales
price of custom built houses is significantly larger than the average sales
price of regular houses. One would expect this to be the case, but it is
valuable to confirm this and to estimate the magnitude of the difference in
average prices if there is one.
There are several tables produced by the two-sample t-test, and the output
looks slightly different when it is printed compared to when it is displayed on
your computer screen. These differences are trivial, however.
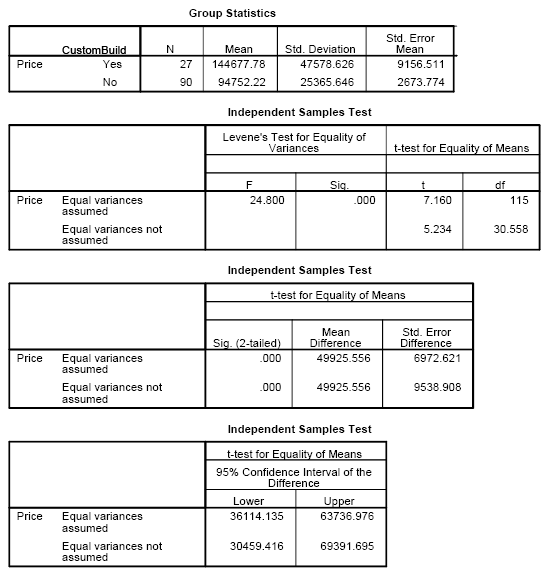
The first table provides descriptive statistics for the two groups. You see that there are 27 custom built
houses and 90 regular houses. The sample means are $145,000 and $95,000 respectively.
The standard deviations are $48,000 and $25,000. Let's not
comment on the standard errors right now.
If you were compiling a table of descriptive statistics, these first few
numbers would be included in that table. Here's one way of presenting that
data.
Custom-built Regular
(n=27) (n=90)
145 +/- 48 95 +/- 25
I always prefer to present the standard deviation rather than the standard
error, but if the journal that you are writing for seems to cite the standard
error more commonly, please follow their convention.
The next set of numbers really bothers me. It presents the Levene's test
for homogeneity. Homogeneity is an assumption required by the traditional
t-test. Homogeneity means that the two populations that you are sampling from
have the same population variance (or equivalently the same population standard
deviations). Heterogeneity occurs when the population variance of one group is
larger or smaller than the population variance of the second group. The
assumption of homogeneity is not a truly critical assumption. The traditional
t-test does just fine if there is a moderate amount of heterogeneity,
especially when the sample sizes are the same in each group.
I do not recommend Levene's test and I would love to find a way to suppress
it. But that is not an option. Please ignore the F value (24.8) and the
p-value (.000). This p-value is frequently and mistakenly presented as the
p-value of the t-test, but it is not.
One of my concerns about Levene's test is that it is overly sensitive, especially for large sample
sizes and can detect trivial amounts of heterogeneity. Levene's test also is
highly influenced by the assumption of normality. So if Levene's test is bad,
what should you do when you are worried that the variances might be unequal? I
recommend that you not worry about this unless there is a strong a priori
reason to believe that the variances might be unequal. Or I recommend that you
assess heterogeneity in a qualitative fashion (is the larger standard
deviation more than three times as big as the smaller population standard
deviation? Is there evidence of heterogeneity in previous closely related
studies?).
The right hand side of the second table, combined with the third table
presents another area of confusion. SPSS reports two t-tests (7.2 and 5.2),
two degrees of freedom (116 and 30.6), two p-values (both, thankfully are .000
but they can sometimes differ), two mean differences (they are always the same
value, here $50,000), two standard errors ($7,000 and $5,200) and two
confidence intervals ($36,000 to $64,000 and $30,000 to $69,000). Which t-test
should you use and how should you I report it.
I recommend that you always use the results in the first row (equal
variances assumed) and ignore the results in the second row (equal variances
not assumed), unless there is a strong a priori reason to believe that there
is serious heterogeneity. A strong a priori reason might come, for example, from previous studies using the same
outcome variable.
Now other people prefer to always use the second row, because it has two
assumptions (independence and normality) rather than the three assumptions needed for the first row
(independence, normality, and homogeneity). Others
will let the results of Levene's test dictate whether to use the equal
variances assumed row or the equal variances not assumed. There's no right or
wrong way to do this, though people will argue endlessly about it. Just use
any of these approaches, but be prepared to adapt to a different approach if a
peer-reviewer requests it.
How should you report these results? It depends. Always report the
confidence interval. Some journals and reviewers like to see the p-value also.
A few places might encourage you to present the t-statistic and the degrees of
freedom. Here's an example of how you might report these results as text in
the results section.
There is a statistically significant difference in average house prices
(95% CI $36,000 to $64,000, p=0.001, t=7.2, df=116).
Note that when SPSS reports a p-value of ".000" it is not exactly zero, but
rather a value that rounds to zero at the third decimal point. I always
convert these p-values to .001.
When I teach people how to use SPSS, I deliberately avoid showing them the
independent samples t-test. Instead, I encourage people to use a more
complicated procedure, the general linear model. I discuss this in detail at
*
www.pmean.com/10/SpssTtest.html
3. The rule of three
The traditional formula for a confidence interval for a proportion uses the
following formula, based on the normal approximation to the binomial
distribution
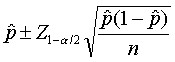
where p-hat is the estimated proportion in the sample. What happens, though,
if the proportion in the sample is zero (no events were observed in your
sample). The formula produces the nonsensical result that the 95% confidence
interval goes from 0 to 0. It reminds me of that Gershwin tune "I've got plenty
of nothing."
How can you create a reasonable confidence interval when you observe zero
events in a sample of size n? It turns out that there is a simple rule of thumb
that works pretty well. If you observe 0 events in a sample of n, then 3/n is an
approximate upper 95% confidence limit for the true proportion in the
population.
Suppose you observe 14 boys undergoing chemotherapy and none of them develop
testicular cancer. What is a 95% confidence interval for the rate of testicular
cancer in boys who have chemotherapy? Using the rule of 3, you get a 95%
confidence interval going up to 3/14=0.214. So you are 95% confident that the
rate of testicular cancer for all boys having chemotherapy is 21% or less.
Let's compare this to an exact calculation of the confidence interval. The
exact interval does not use a simple formula and requires specialized software. The
following is an excerpt from the output of a computer program, StatXact, that
computes exact confidence intervals for a proportion for any sample size and any
number of events.
Number of Trials =14 Number of Successes =0
Point Estimation of PI = 0.0000
95.00% Confidence Interval for PI = ( 0.0000 , 0.2316)
We see that the exact confidence interval extends up to 23%. So even with
only 14 patients, our approximate confidence interval based on the rule of 3 is
not off by too much. As the sample size increases, this approximation gets
better and better.
You can see a mathematical derivation of the rule of three at:
*
www.pmean.com/01/zeroevents.html
4. Monthly Mean Article (peer reviewed): When Intuition
And Math Probably Look Wrong
Both articles in this month's newsletter deal with classic probability
puzzles.
Julie Rehmeyer. When Intuition And Math Probably Look Wrong. Science News (web edition). Excerpt: "I have two children, one of
whom is a son born on a Tuesday. What is the probability that I have two boys?
Gary Foshee, a puzzle designer from Issaquah, Wash., posed this puzzle during
his talk this past March at Gathering 4 Gardner, a convention of
mathematicians, magicians and puzzle enthusiasts held biannually in Atlanta.
The convention is inspired by Martin Gardner, the recreational mathematician,
expositor and philosopher who died May 22 at age 95. Foshee�s riddle is a
beautiful example of the kind of simple, surprising and sometimes
controversial bits of mathematics that Gardner prized and shared with others."
[Accessed July 5, 2010]. Available at:
http://sciencenews.org/view/generic/id/60598/title/When_intuition_and_math_probably_look_wrong.
5. Monthly Mean Article (popular press): Numberplay: Your
Money or Your Logic
Gary Antonick, Numberplay: Your Money or Your Logic, New York Times
(online edition), July 5, 2010. Excerpt: "We tend to make pretty good decisions.
Whipped cream on that? Sure. Jill Denny and Jeff Chen crossword? Double sure. We
don�t even have to think about it. Sometimes, however, we do have to think about
it. Say you have a dollar. A friend with two dollars and a coin proposes a game:
give her your dollar and she�ll flip. Heads, you can have all three dollars.
Tails, nothing. So there�s a 50 percent chance you�ll triple your money. Yow.
Three dollars is pretty mad cash. But you could lose everything. What�s the
logical way to think about this?"
http://wordplay.blogs.nytimes.com/2010/07/05/numberplay-your-money-or-your-logic
6. Monthly Mean Book: Health measurement scales
David L Streiner, Geoffrey R Norman. Health measurement scales. 4th ed. New
York: Oxford University Press; 2008. Developing a new measurement scale is not a
trivial undertaking. You can't just toss a bunch of questions together and
expect them to measure something meaningful like stress or quality of life.
Developing a measurement scale is a long and elaborate process with multiple
studies attempting to establish reliability and validity. This book offers an
outstanding overview of this process.
7. Monthly Mean Definition: What is a fishbone diagram?
The fishbone diagram (also called the Ishikawa diagram, or the case and
effect diagram) is a tool for identifying the root causes of quality problems.
It was named after Kaoru Ishikawa, the man who pioneered the use of this chart
in quality improvement in the 1960's. It is a graphical method for displaying
possible causes of a quality problem.
If you want to use a Fishbone Diagram, first list the main problem on the
right hand side of the paper. Then draw a horizontal line to represent the
"backbone" of the diagram. This line is not labeled.
Off of the backbone, draw and label major bones: 4 to 7 major categories of
causes. A commonly used list of major causes is
* Management,
* Manpower,
* Machines, and
* Materials.
Another possible list is
* Policies,
* Procedures,
* Plant, and
* People.
Then attach specific causes to the appropriate category.
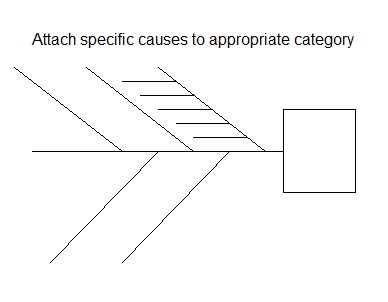
Some people allow the individual causes to have subcauses, which would be attached to the minor bones. This is
intended to get at the fundamental or root causes of the problem. Other people
do not include this level of detail on their fishbone diagrams.
The process of developing a fishbone diagram can be done by an individual,
but more commonly it is done by a team. You can use standard brainstorming
approaches for the fishbone diagram. For example you could go around the table
repeatedly asking each person to list a cause. Only after all the possible
causes are listed do you review and possibly winnow down the list. Then arrange
the remaining causes on the fishbone.
If you do use a team to develop a fishbone diagram, make sure that all
relevant parties are included. No fair getting input only from doctors and
ignoring nurses, for example, in a health care setting. The rule should be that
at least one person from any group that is associated with the work process
should be included.
When you are done, look at the entire diagram. Does it have reasonable
balance across the major bones? Are any common themes emerging? Can you identify
causes that are measurable and fixable and which you believe are likely to have
a large impact on the problem?
In some situations, you may find that a flow diagram of the work process may
be more valuable and informative.
There are several interesting examples of Fishbone diagrams on the web:
*
www.gerald-suarez.com/img/fishbone_large.png
*
www.leankaizen.co.uk/images/free%20stuff%20fishbone%20diagram%20web.jpg
*
www.geekpreneur.com/wp-content/uploads/2008/07/fishbone.jpg
*
www.spcforexcel.com/files/images/fishbone1.gif
8. Monthly Mean Quote: The government is extremely
fond...
"The government is extremely fond of amassing great quantities of statistics.
These are raised to the Nth degree, the cube roots are extracted, and the
results are arranged into elaborate and impressive displays. What must be kept
ever in mind, however, is that in every case, the figures are first put down by
a village watchman, and he puts down anything he damn well pleases." Sir Josiah
Stamp, as quoted at
http://www.daclarke.org/AltTrans/BadScience.html.
9. Monthly Mean Unsung Hero Award: Ed Rigdon
Ed Rigdon maintains the frequently asked questions list for Structural
Equations Modeling (SEM) at http://www2.gsu.edu/~mkteer/semfaq.html.
This is an outstanding resource. Let me reproduce the answer to the very basic
question "What is SEM?" to show the quality of his writing.
Structural equation modeling, or SEM, is a very general, chiefly linear,
chiefly cross-sectional statistical modeling technique. Factor analysis, path
analysis and regression all represent special cases of SEM.
SEM is a largely confirmatory, rather than exploratory, technique. That
is, a researcher are more likely to use SEM to determine whether a certain model
is valid., rather than using SEM to "find" a suitable model--although SEM
analyses often involve a certain exploratory element.
In SEM, interest usually focuses on latent constructs--abstract
psychological variables like "intelligence" or "attitude toward the
brand"--rather than on the manifest variables used to measure these constructs.
Measurement is recognized as difficult and error-prone. By explicitly modeling
measurement error, SEM users seek to derive unbiased estimates for the relations
between latent constructs. To this end, SEM allows multiple measures to be
associated with a single latent construct.
A structural equation model implies a structure of the covariance matrix
of the measures (hence an alternative name for this field, "analysis of
covariance structures"). Once the model's parameters have been estimated, the
resulting model-implied covariance matrix can then be compared to an empirical
or data-based covariance matrix. If the two matrices are consistent with one
another, then the structural equation model can be considered a plausible
explanation for relations between the measures.
Compared to regression and factor analysis, SEM is a relatively young
field, having its roots in papers that appeared only in the late 1960s. As such,
the methodology is still developing, and even fundamental concepts are subject
to challenge and revision. This rapid change is a source of excitement for some
researchers and a source of frustration for others.
Maintaining an FAQ is a tedious and largely thankless task. The SEM community
in particular, and the research community in general is indebted to Dr. Rigdon
for this work.
10. Monthly Mean Website: Research Papers on Inter-Rater Reliability Estimation
Kilem Li Gwet. Research Papers on Inter-Rater Reliability Estimation.
Excerpt: "Below are some downloadable research papers published by Dr. Gwet
on Inter-Rater Reliability. They are all in PDF format." [Accessed July 7,
2010]. Available at:
http://www.agreestat.com/research_papers.html.
11. Nick News: Nicholas carries a big chunk of the
Mendenhall glacier
While in Juneau, we took a bus tour to Mendenhall Glacier. It was the first
glacier that I saw on our Alaska tour, and it was quite impressive. Pieces of
the glacier had fallen off into Mendenhall Lake and Nicholas found one that
had drifted ashore. At first, I told Nicholas that he needed to leave the chunk of ice right
there. But then we found that the park rangers had taken another chunk of ice
from the lake and were displaying it near the visitors center. So Nicholas
wanted to bring them his own chunk of ice.

See more pictures at
*
www.pmean.com/personal/Mendenhall.html
12. Very bad joke: How many statisticians...
How many statisticians does it take to light a gas stove? I don't know
because we haven't run the pilot study yet.
This is an original joke, but it may show how old I actually am to remember
things like pilot lights on a gas stove.
13. Tell me what you think.
How did you like this newsletter? I have three short open ended questions at
*
https://app.icontact.com/icp/sub/survey/start?sid=6356&cid=338122
You can also provide feedback by responding to this email. My three
questions are:
- What was the most important thing that you learned in this newsletter?
- What was the one thing that you found confusing or difficult to follow?
- What other topics would you like to see covered in a future newsletter?
Three people provided feedback to the last newsletter. I got compliments on
the article about why randomization doesn't always work, about Simpson's paradox
(I think this person was thinking about my interaction article), and the link to
the journal article about overdiagnosis of cancer. Several people were confused,
though, about the description of interactions among two continuous variables in
a linear regression model. I'll see if I can simplify it. There weren't a lot of
suggestions about future topics and one person liked being surprised. A comment
about the advantages of meta-analysis over simply counting the number of
positive/negative studies was offered, though.
P.S. The process of creating these newsletters is to forget about them for
long stretches of time, then notice that an entire month has passed, or
sometimes two months. Then I rush to write a bunch of things so that I can
still justify the adjective "Monthly" in my newsletter title. I realized just
now that I don't review earlier suggestions about future topics when I am in a
panic writing mode. I apologize. I have collated the suggestions that you have
made over the past two years and keep them in my "filler" file where I store
ideas for future newsletter topics. I will try harder to address some of your
suggestions, but keep in mind that some of the topics you have suggested are
quite difficult to write about.
14. Upcoming statistics webinars
I offer regular webinars (web seminars) for free as a service to the research
community and to build up a bit of good will for my independent consulting
business.
The first three steps in a linear regression analysis with examples in IBM SPSS.
Wednesday, July 14, 11am CDT. Abstract: This class will give you a
general introduction in how to use SPSS software to compute linear regression
models. Linear regression models provide a good way to examine how various
factors influence a continuous outcome measure. There are three steps in a
typical linear regression analysis: fit a crude model, fit an adjusted model,
and check your assumptions These steps may not be appropriate for every linear
regression analysis, but they do serve as a general guideline. In this class
you will learn how to: interpret the slope and intercept in a linear
regression model; compute a simple linear regression model; and make
statistical adjustments for covariates.
The first three steps in a logistic regression analysis with examples in
IBM SPSS. Thursday, July 15, 11am CDT. Abstract: This training class will
give you a general introduction in how to use IBM SPSS software to compute
logistic regression models. Logistic regression models provide a good way to
examine how various factors influence a binary outcome. There are three steps
in a typical logistic regression analysis: First, fit a crude model. Second,
fit an adjusted model. Third, examine the predicted probabilities. These steps
may not be appropriate for every logistic regression analysis, but they do
serve as a general guideline. In this presentation, you will see these steps
applied to data from a breast feeding study, using SPSS software. Objectives:
In this class, you will learn how to compute and interpret simple odds ratios;
and relate the output of a logistic regression model to these odds ratios.
Data entry and data management issues with examples in IBM SPSS. Tuesday,
August 24, 11am CDT. Abstract: This training class will give you a general introduction
to data management using IBM SPSS software. This class is useful for anyone
who needs to enter or analyze research data. There are three steps that will
help you get started with data entry for a research project. First, arrange
your data in a rectangular format (one and only one number in each
intersection of every row and column). Second, create a name for each column
of data and provide documentation on this column such as units of measurement.
Third, create codes for categorical data and for missing values. This class
will show examples of data entry including the tricky issues associated with
data entry of a two by two table and entry of dates.
To sign up for any of these, send me an email with the date of the webinar
in the title line (e.g., "April 28 webinar"). For further information, go to
* www.pmean.com/webinars
15. Join me on Facebook and LinkedIn
I'm just getting started with Facebook and LinkedIn. My personal page on
Facebook is
* www.facebook.com/pmean
and there is a fan page for The Monthly Mean
*
www.facebook.com/group.php?gid=302778306676
I usually put technical stuff on the Monthly Mean fan page and personal stuff
on my page, but there's a bit of overlap.
My page on LinkedIn is
* www.linkedin.com/in/pmean
If you'd like to be a friend on Facebook or a connection on LinkedIn, I'd
love to add you.
What now?
Sign up for the Monthly Mean newsletter
Review the archive of Monthly Mean newsletters
Go to the main page of the P.Mean website
Get help
 This work is licensed under a
Creative
Commons Attribution 3.0 United States License. This page was written by
Steve Simon and was last modified on
2017-06-15. Need more
information? I have a page with general help
resources. You can also browse for pages similar to this one at
Category: Website details.
This work is licensed under a
Creative
Commons Attribution 3.0 United States License. This page was written by
Steve Simon and was last modified on
2017-06-15. Need more
information? I have a page with general help
resources. You can also browse for pages similar to this one at
Category: Website details.