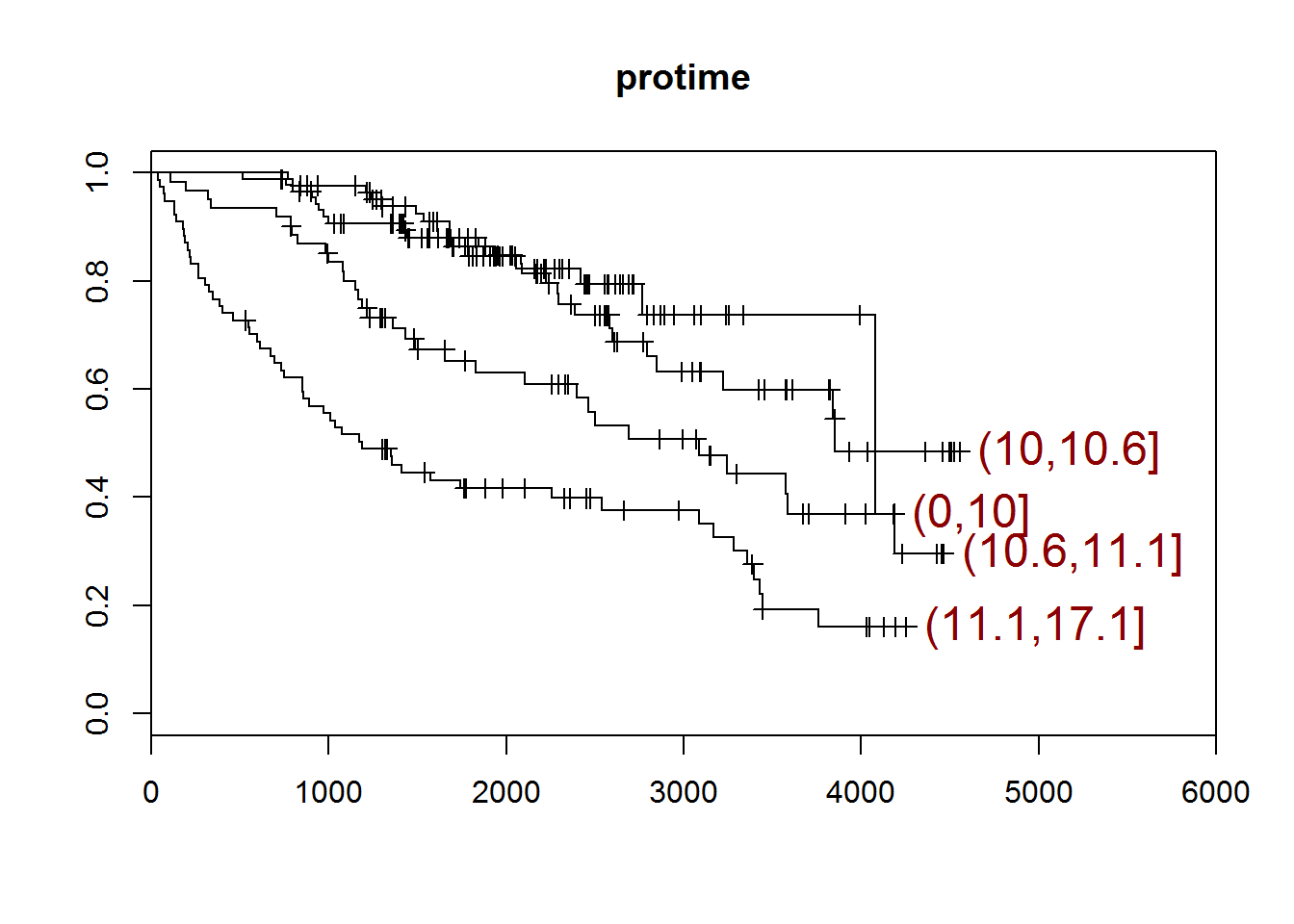
I found a larger data set and wanted to show how you could use the Kaplan Meier curves as a preliminary screen of some categorical and continuous variables in a larger and more complex data set.
I am building on a previous blog entry and this referred to an earlier webpage. Here is the R code. The comment section at the top is a cut-and-paste from the documentation of the data file.
# Some simple examples of survival analysis
# The data set is a study of primary biliary cirrhosis
# Variables:
# V1 case number
# V2 number of days between registration and the earlier of death,
# transplantion- or study analysis time in July
- 1986 # V3 status # 0=censored
- 1=censored due to liver tx
- 2=death # V4 drug # 1= D-penicillamine
- 2=placebo # V5 age in days # V6 sex # 0=male
- 1=female # V7 presence of asictes # 0=no 1=yes # V8 presence of hepatomegaly # 0=no 1=yes # V9 presence of spiders # 0=no 1=yes # V10 presence of edema
# 0 = no edema and no diuretic therapy for edema; # 0.5 = edema present without diuretics - or edema resolved by diuretics; # 1 = edema despite diuretic therapy # V11 serum bilirubin in mg/dl # V12 serum cholesterol in mg/dl # V13 albumin in gm/dl # V14 urine copper in ug/day# # V15 alkaline phosphatase in U/liter # V16 SGOT in U/ml # V17 triglicerides in mg/dl # V18 platelets per cubic ml / 1000 # V19 prothrombin time in seconds # V20 histologic stage of disease
Read the data in from the website. The first 60 rows are documentation about the file and the actual data starts on line 61.
fn <- "http://lib.stat.cmu.edu/datasets/pbc"
pbc <- read.table(fn,header=FALSE,skip=60)
head(pbc)
V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V15 V16 V17 V18 V19 V20
1 1 400 2 1 21464 1 1 1 1 1.0 14.5 261 2.60 156 1718.0 137.95 172 190 12.2 4
2 2 4500 0 1 20617 1 0 1 1 0.0 1.1 302 4.14 54 7394.8 113.52 88 221 10.6 3
3 3 1012 2 1 25594 0 0 0 0 0.5 1.4 176 3.48 210 516.0 96.10 55 151 12.0 4
4 4 1925 2 1 19994 1 0 1 1 0.5 1.8 244 2.54 64 6121.8 60.63 92 183 10.3 4
5 5 1504 1 2 13918 1 0 1 1 0.0 3.4 279 3.53 143 671.0 113.15 72 136 10.9 3
6 6 2503 2 2 24201 1 0 1 0 0.0 0.8 248 3.98 50 944.0 93.00 63 . 11.0 3The data looks like it read in properly - so let’s load the survival library.
> library("survival")
Loading required package: splines
Attaching package: <U+0091>survival<U+0092>
The following object is masked _by_ <U+0091>.GlobalEnv<U+0092>:
pbcNow that’s strange. There is an object in the survival library that has the same name (pbc). Let’s investigate.
> rm(pbc)
> head(pbc)
id time status trt age sex ascites hepato spiders edema bili chol albumin copper alk.phos
1 1 400 2 1 58.76523 f 1 1 1 1.0 14.5 261 2.60 156 1718.0
2 2 4500 0 1 56.44627 f 0 1 1 0.0 1.1 302 4.14 54 7394.8
3 3 1012 2 1 70.07255 m 0 0 0 0.5 1.4 176 3.48 210 516.0
4 4 1925 2 1 54.74059 f 0 1 1 0.5 1.8 244 2.54 64 6121.8
5 5 1504 1 2 38.10541 f 0 1 1 0.0 3.4 279 3.53 143 671.0
6 6 2503 2 2 66.25873 f 0 1 0 0.0 0.8 248 3.98 50 944.0
ast trig platelet protime stage
1 137.95 172 190 12.2 4
2 113.52 88 221 10.6 3
3 96.10 55 151 12.0 4
4 60.63 92 183 10.3 4
5 113.15 72 136 10.9 3
6 93.00 63 NA 11.0 3Wow! The data set I was importing was already part of the survival library. Let’s use their version - since it has better names for the variables than V1-V20.
We have to subset the data because the first 312 observations represent a randomized trial and the remaining observations are an add-on study of baseline values for some non-randomized patients.
> tail(pbc)
id time status trt age sex ascites hepato spiders edema bili chol albumin copper
413 413 989 0 NA 35.00068 f NA NA NA 0 0.7 NA 3.23 NA
414 414 681 2 NA 67.00068 f NA NA NA 0 1.2 NA 2.96 NA
415 415 1103 0 NA 39.00068 f NA NA NA 0 0.9 NA 3.83 NA
416 416 1055 0 NA 56.99932 f NA NA NA 0 1.6 NA 3.42 NA
417 417 691 0 NA 58.00137 f NA NA NA 0 0.8 NA 3.75 NA
418 418 976 0 NA 52.99932 f NA NA NA 0 0.7 NA 3.29 NA
alk.phos ast trig platelet protime stage
413 NA NA NA 312 10.8 3
414 NA NA NA 174 10.9 3
415 NA NA NA 180 11.2 4
416 NA NA NA 143 9.9 3
417 NA NA NA 269 10.4 3
418 NA NA NA 350 10.6 4
> pmod <- pbc[1:312,]
> tail(pmod)
id time status trt age sex ascites hepato spiders edema bili chol albumin copper
307 307 1149 0 2 30.57358 f 0 0 0 0 0.8 273 3.56 52
308 308 1153 0 1 61.18275 f 0 1 0 0 0.4 246 3.58 24
309 309 994 0 2 58.29979 f 0 0 0 0 0.4 260 2.75 41
310 310 939 0 1 62.33265 f 0 0 0 0 1.7 434 3.35 39
311 311 839 0 1 37.99863 f 0 0 0 0 2.0 247 3.16 69
312 312 788 0 2 33.15264 f 0 0 1 0 6.4 576 3.79 186
alk.phos ast trig platelet protime stage
307 1282 130 59 344 10.5 2
308 797 91 113 288 10.4 2
309 1166 70 82 231 10.8 2
310 1713 171 100 234 10.2 2
311 1050 117 88 335 10.5 2
312 2115 136 149 200 10.8 2Take a look at the two key variables needed to define the survival object. Dividing by 365.25 gives the times in years rather than in days.
> summary(pmodtime)
Min. 1st Qu. Median Mean 3rd Qu. Max.
41 1191 1840 2006 2697 4556
> summary(pmodtime/365.25)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.1123 3.2610 5.0360 5.4930 7.3850 12.4700
> table(pmodstatus)
0 1 2
168 19 125The values for status - if you read the documentation - are 0=censored, 1=transplant - and 2=death. You could define an event as either 1 and 2 or 2 by itself. Choose the latter for this example.
> p.surv >- Surv(pmodtime,pmod$status==2)
print(p.surv)
[1] 400 4500+ 1012 1925 1504+ 2503 1832+ 2466 2400 51 3762 304 3577+ 1217 3584
[16] 3672+ 769 131 4232+ 1356 3445+ 673 264 4079 4127+ 1444 77 549 4509+ 321
[31] 3839 4523+ 3170 3933+ 2847 3611+ 223 3244 2297 4467+ 1350 4453+ 4556+ 3428 4025+
[46] 2256 2576+ 4427+ 708 2598 3853 2386 1000 1434 1360 1847 3282 4459+ 2224 4365+
[61] 4256+ 3090 859 1487 3992+ 4191 2769 4039+ 1170 3458+ 4196+ 4184+ 4190+ 1827 1191
[76] 71 326 1690 3707+ 890 2540 3574 4050+ 4032+ 3358 1657 198 2452+ 1741 2689
[91] 460 388 3913+ 750 130 3850+ 611 3823+ 3820+ 552 3581+ 3099+ 110 3086 3092+
[106] 3222 3388+ 2583 2504+ 2105 2350+ 3445 980 3395 3422+ 3336+ 1083 2288 515 2033+
[121] 191 3297+ 971 3069+ 2468+ 824 3255+ 1037 3239+ 1413 850 2944+ 2796 3149+ 3150+
[136] 3098+ 2990+ 1297 2106+ 3059+ 3050+ 2419 786 943 2976+ 2615+ 2995+ 1427 762 2891+
[151] 2870+ 1152 2863+ 140 2666+ 853 2835+ 2475+ 1536 2772+ 2797+ 186 2055 264 1077
[166] 2721+ 1682 2713+ 1212 2692+ 2574+ 2301+ 2657+ 2644+ 2624+ 1492 2609+ 2580+ 2573+ 2563+
[181] 2556+ 2555+ 2241+ 974 2527+ 1576 733 2332+ 2456+ 2504+ 216 2443+ 797 2449+ 2330+
[196] 2363+ 2365+ 2357+ 1592+ 2318+ 2294+ 2272+ 2221+ 2090 2081 2255+ 2171+ 904 2216+ 2224+
[211] 2195+ 2176+ 2178+ 1786 1080 2168+ 790 2170+ 2157+ 1235 2050+ 597 334 1945+ 2022+
[226] 1978+ 999 1967+ 348 1979+ 1165 1951+ 1932+ 1776+ 1882+ 1908+ 1882+ 1874+ 694 1831+
[241] 837+ 1810+ 930 1690 1790+ 1435+ 732+ 1785+ 1783+ 1769+ 1457+ 1770+ 1765+ 737+ 1735+
[256] 1701+ 1614+ 1702+ 1615+ 1656+ 1677+ 1666+ 1301+ 1542+ 1084+ 1614+ 179 1191 1363+ 1568+
[271] 1569+ 1525+ 1558+ 1447+ 1349+ 1481+ 1434+ 1420+ 1433+ 1412+ 41 1455+ 1030+ 1418+ 1401+
[286] 1408+ 1234+ 1067+ 799 1363+ 901+ 1329+ 1320+ 1302+ 877+ 1321+ 533+ 1300+ 1293+ 207
[301] 1295+ 1271+ 1250+ 1230+ 1216+ 1216+ 1149+ 1153+ 994+ 939+ 839+ 788+First - let’s look at an overall survival curve.
> plot(survfit(p.surv~1))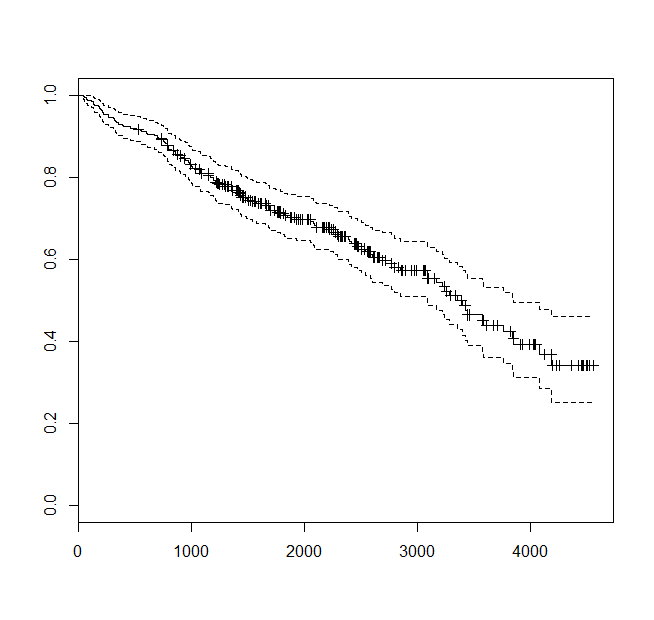
Now let’s define some functions that will calculate and compare Kaplan-Meier curves across all the possible covariates in the model. For categorical variables - draw Kaplan-Meier curves for each category level. For continuous variables - split the data into quartiles and then draw Kaplan-Meier curves for each quartile.
km.cat <- function(vn) {
print(vn)
print(table(pmod[,vn]))
km.all(pmod[,vn])
title(vn)
}
km.con <- function(vn) {
print(vn)
br <- quantile(pmod[,vn],na.rm=TRUE)
br[1] <- 0
quartiles <- cut(pmod[,vn],breaks=br)
print(table(quartiles))
km.all(quartiles)
title(vn)
}
km.all <- function(x) {
tb <- table(x)
mi <- sum(is.na(x))
sf <- survfit(p.surv~x)
print(paste("There are",mi,"missing values."))
plot(sf,xlim=c(0,6000))
end.pts <- cumsum(sfstrata)
end.x <- sftime[end.pts]+100
end.y <- sfsurv[end.pts]
end.nm <- names(tb)
text(end.x,end.y,end.nm,cex=1.5,col="darkred",adj=0)
}
v.cat <- names(pmod)[c(4,6:10,20)]
v.con <- names(pmod)[c(5,11:19)]
for (v in v.cat) {
km.cat(v)
}
for (v in v.con) {
km.con(v)
}Here is the output.
v.cat <- names(pmod)[c(4,6:10,20)]
v.con <- names(pmod)[c(5,11:19)]
for (v in v.cat) {
km.cat(v)
}## [1] "trt"
##
## 1 2
## 158 154
## [1] "There are 0 missing values."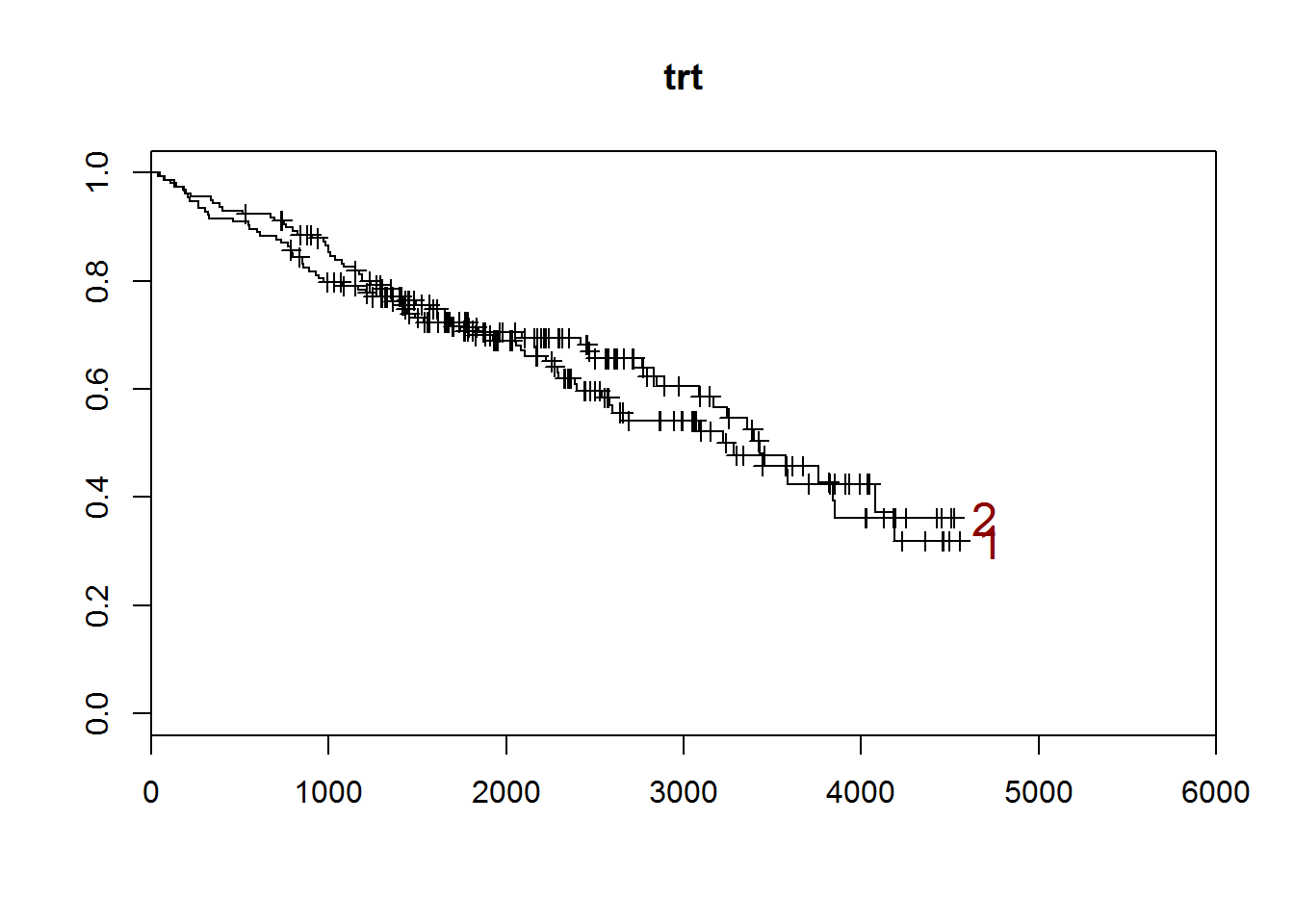
## [1] "sex"
##
## m f
## 36 276
## [1] "There are 0 missing values."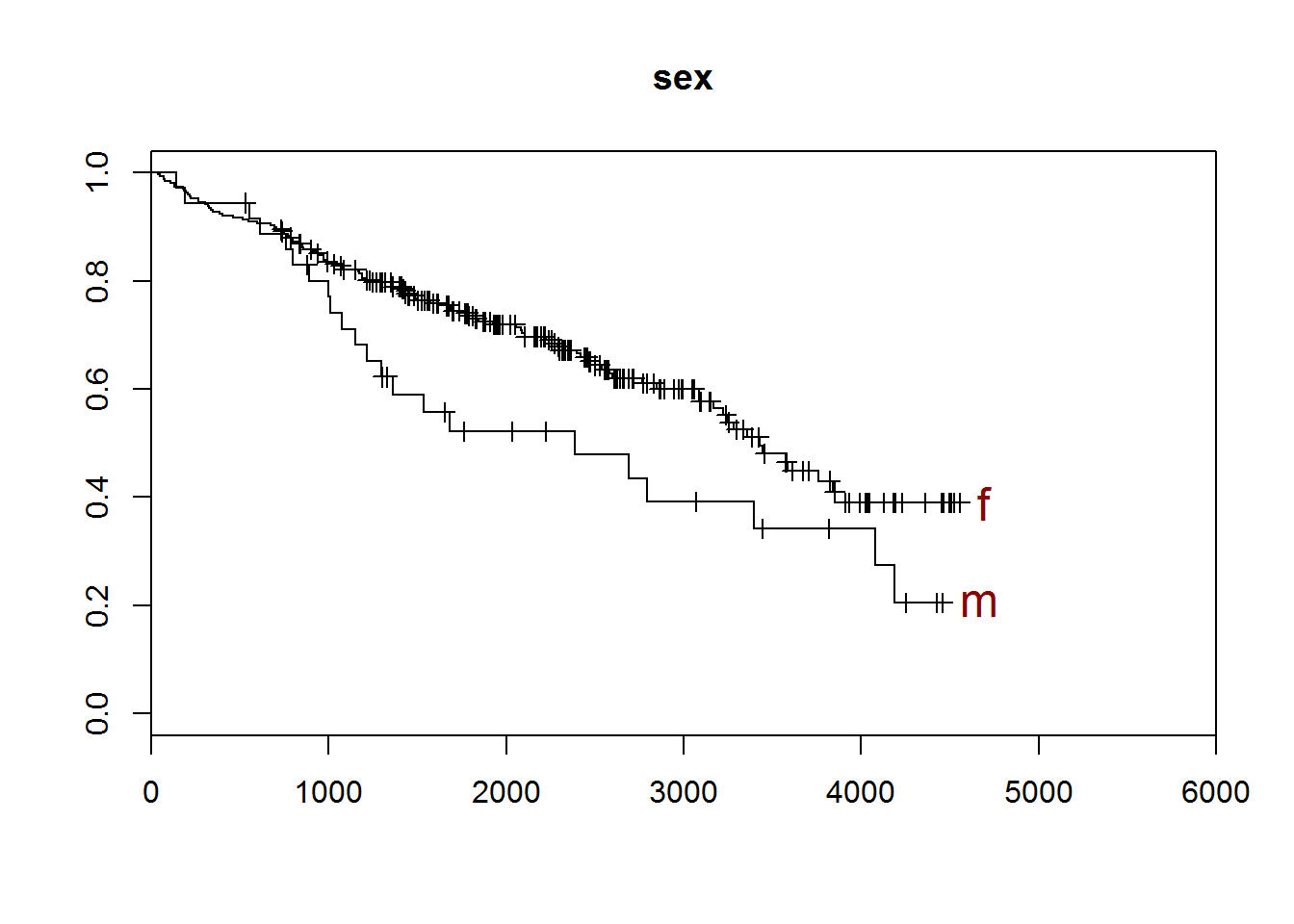
## [1] "ascites"
##
## 0 1
## 288 24
## [1] "There are 0 missing values."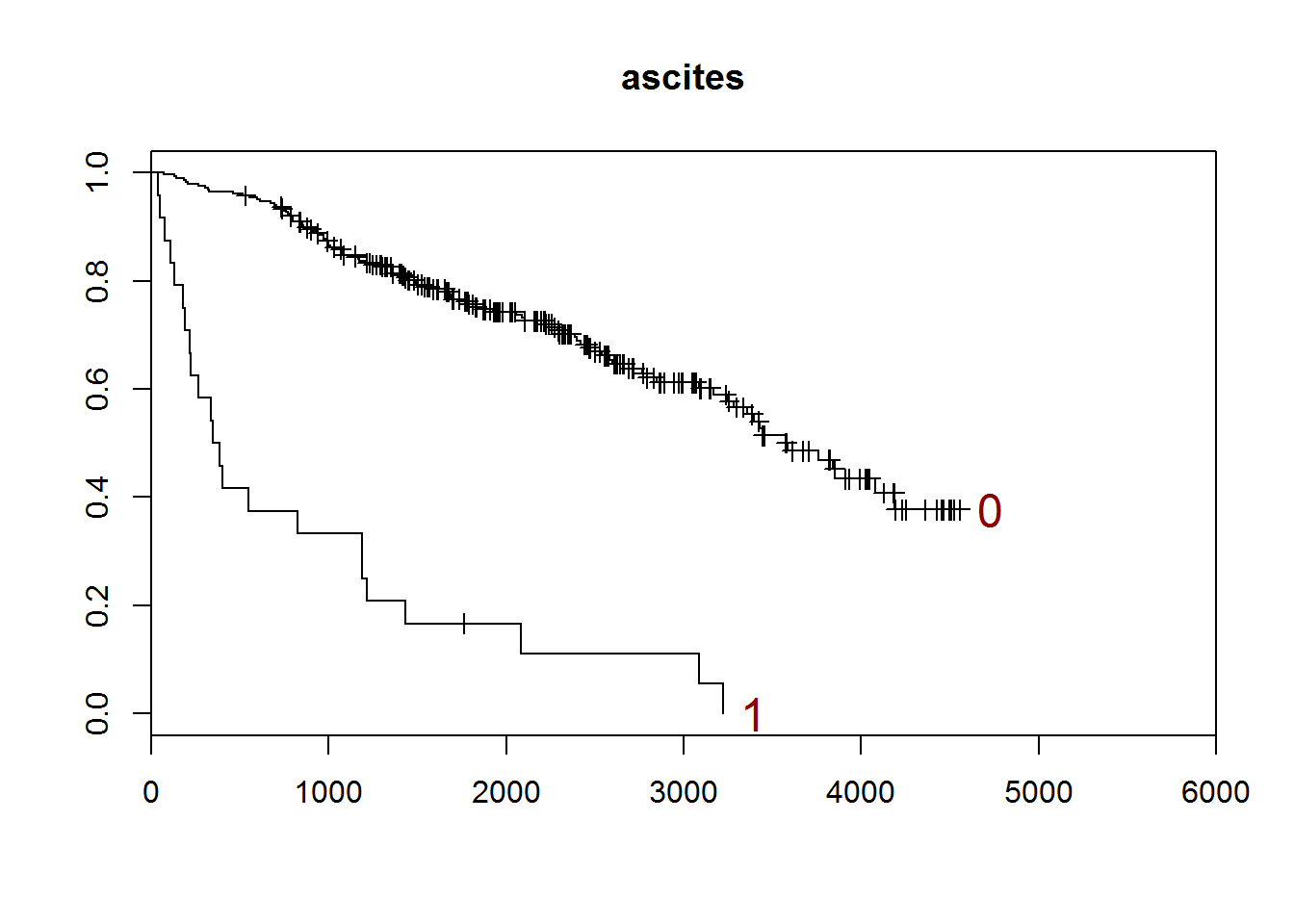
## [1] "hepato"
##
## 0 1
## 152 160
## [1] "There are 0 missing values."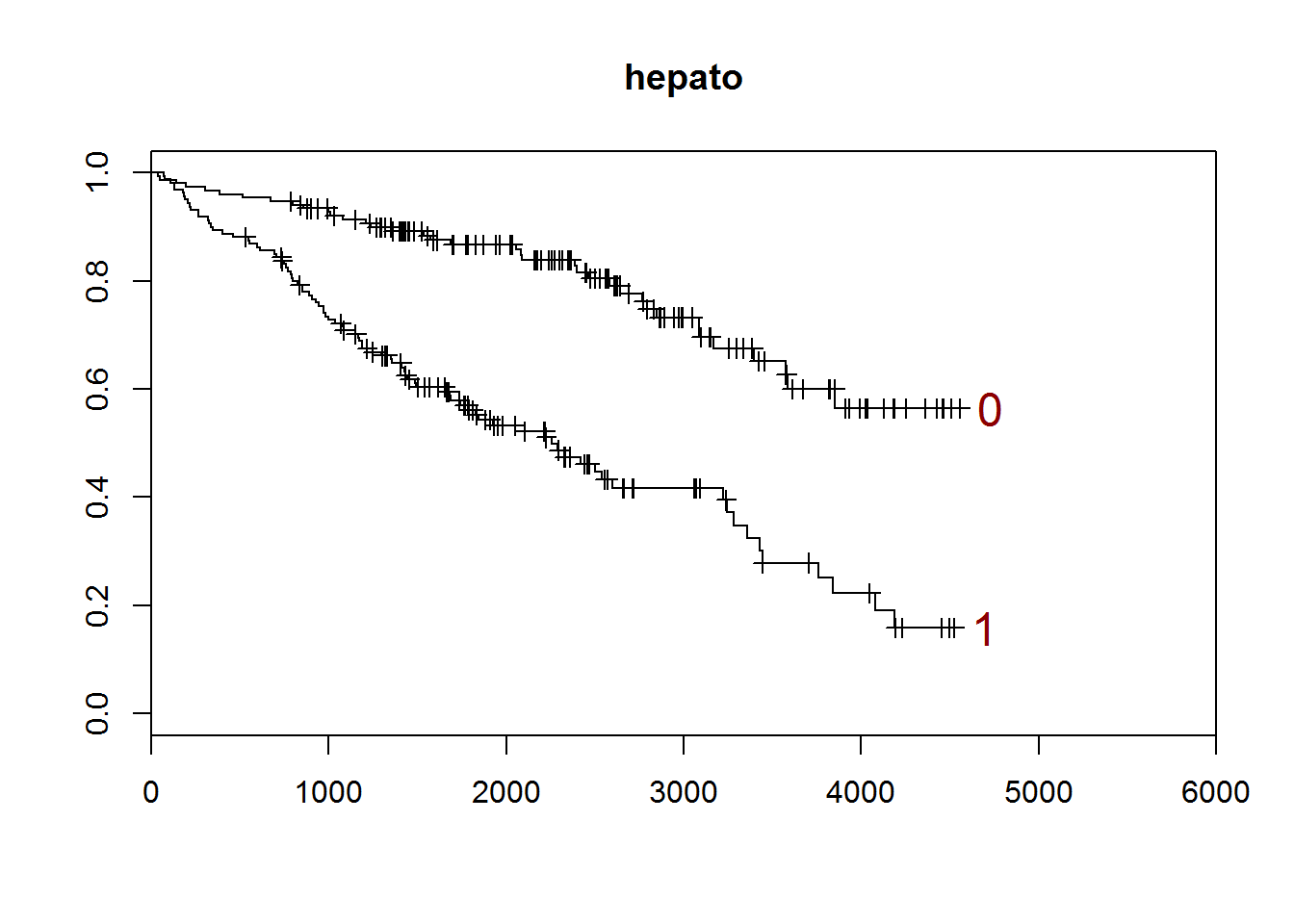
## [1] "spiders"
##
## 0 1
## 222 90
## [1] "There are 0 missing values."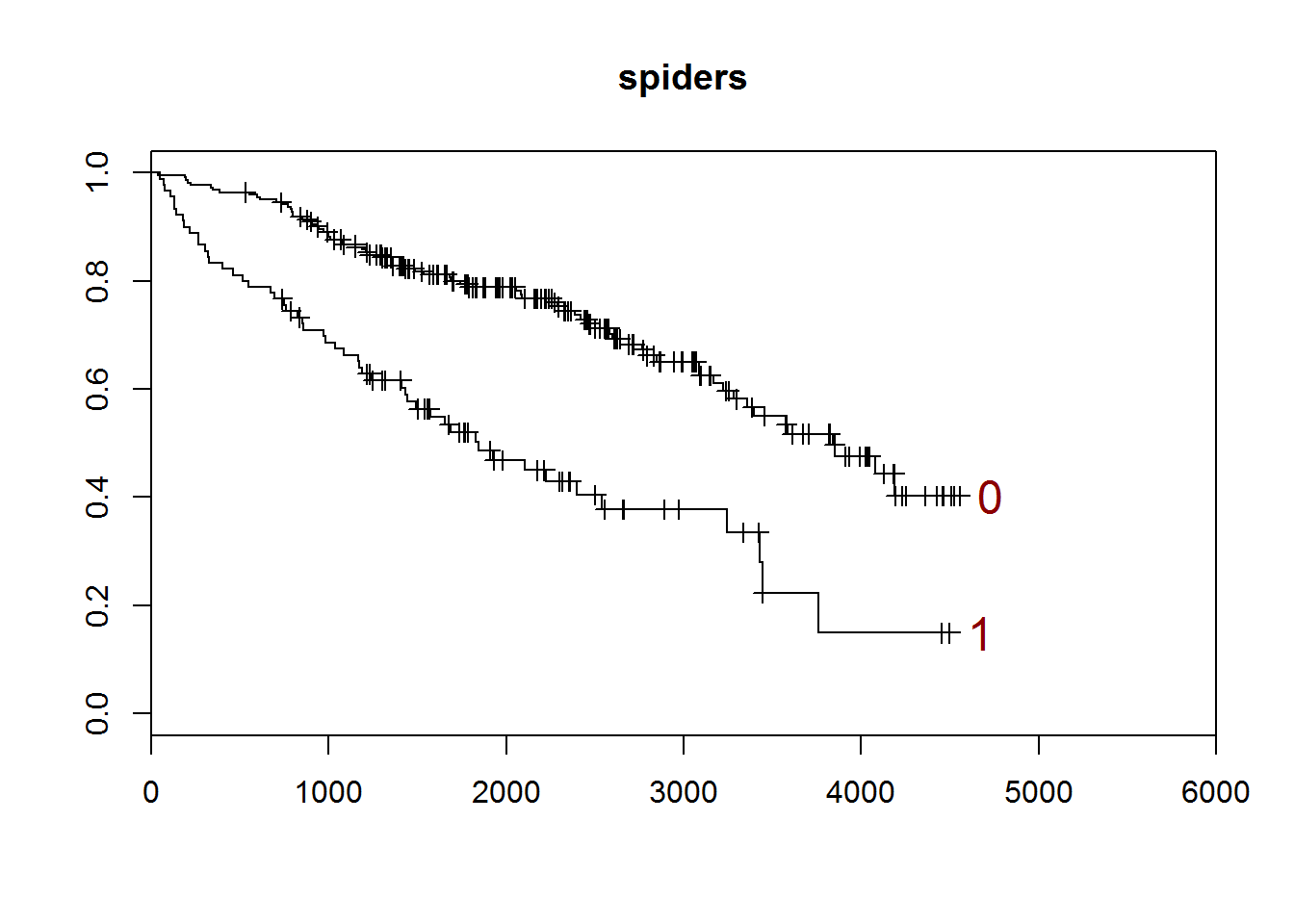
## [1] "edema"
##
## 0 0.5 1
## 263 29 20
## [1] "There are 0 missing values."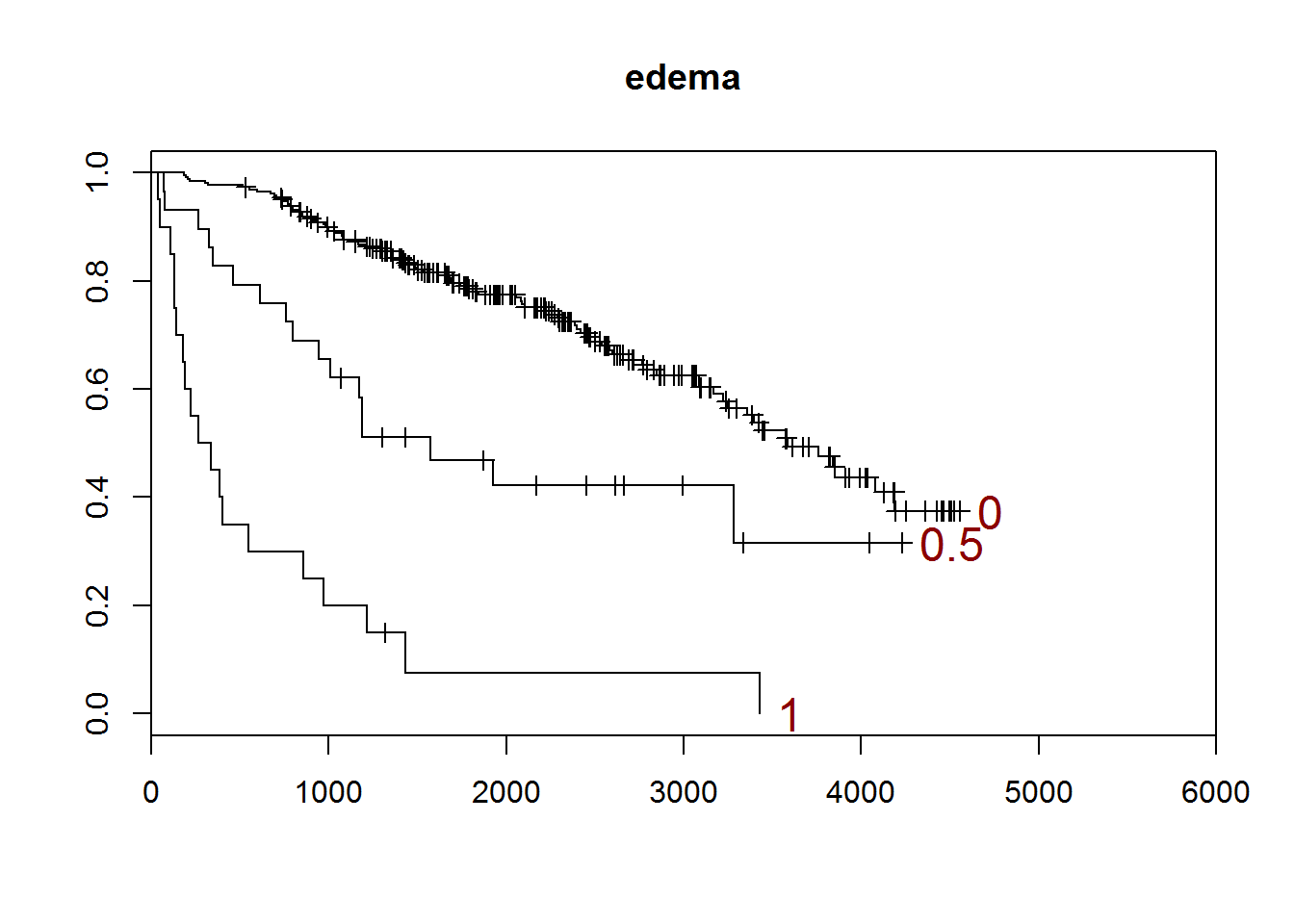
## [1] "stage"
##
## 1 2 3 4
## 16 67 120 109
## [1] "There are 0 missing values."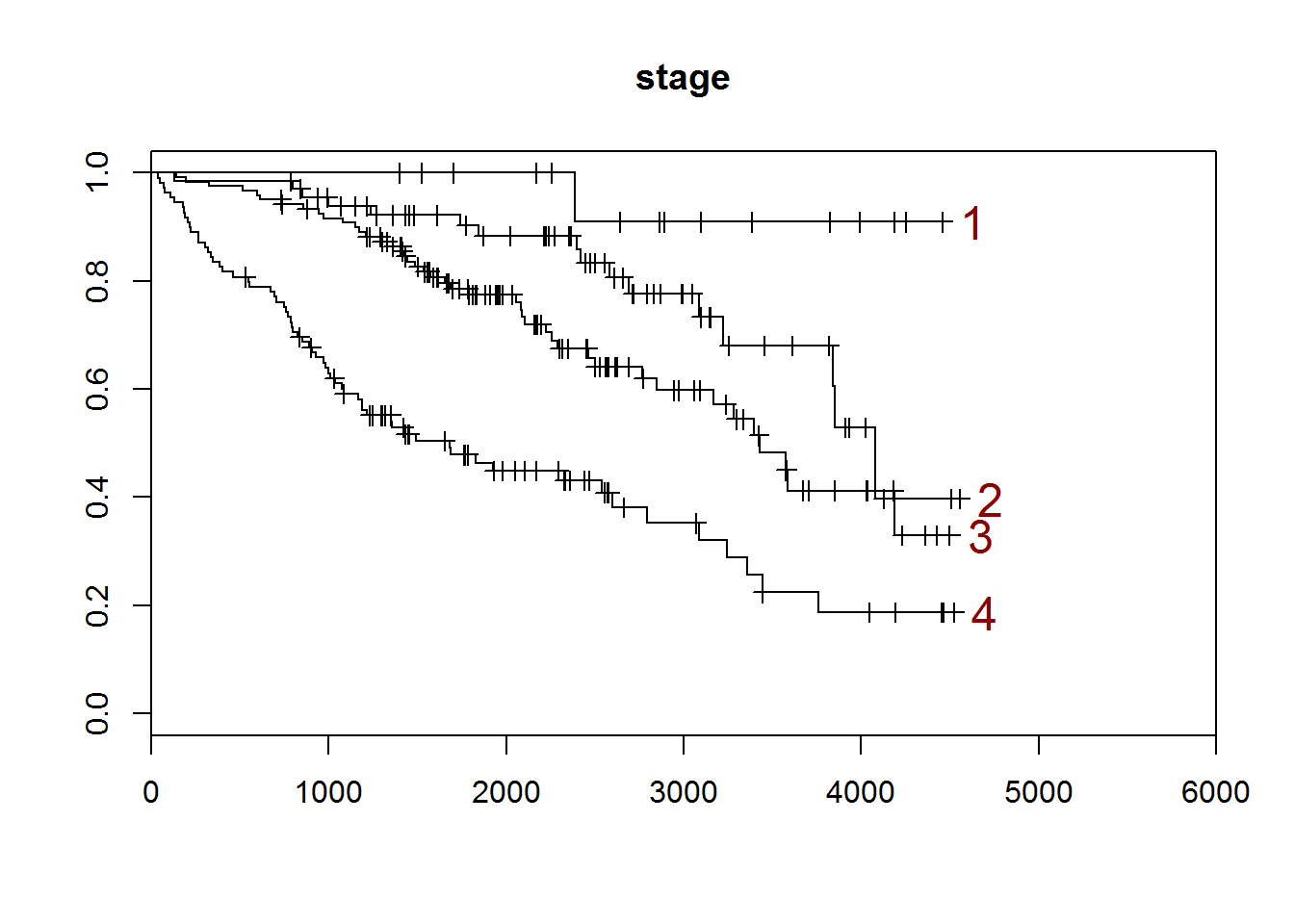
for (v in v.con) {
km.con(v)
}## [1] "age"
## quartiles
## (0,42.2] (42.2,49.8] (49.8,56.7] (56.7,78.4]
## 78 78 78 78
## [1] "There are 0 missing values."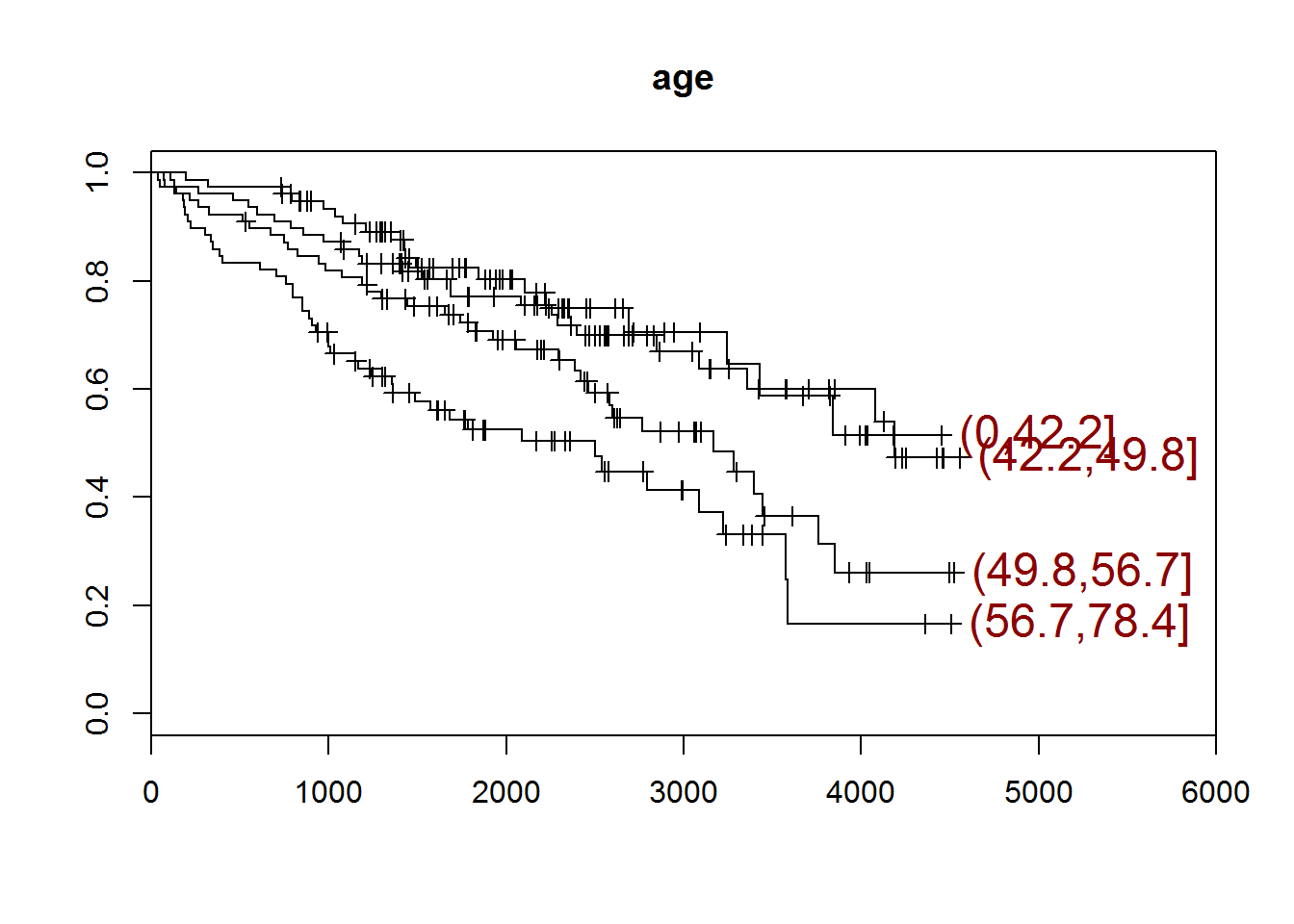
## [1] "bili"
## quartiles
## (0,0.8] (0.8,1.35] (1.35,3.42] (3.42,28]
## 90 66 78 78
## [1] "There are 0 missing values."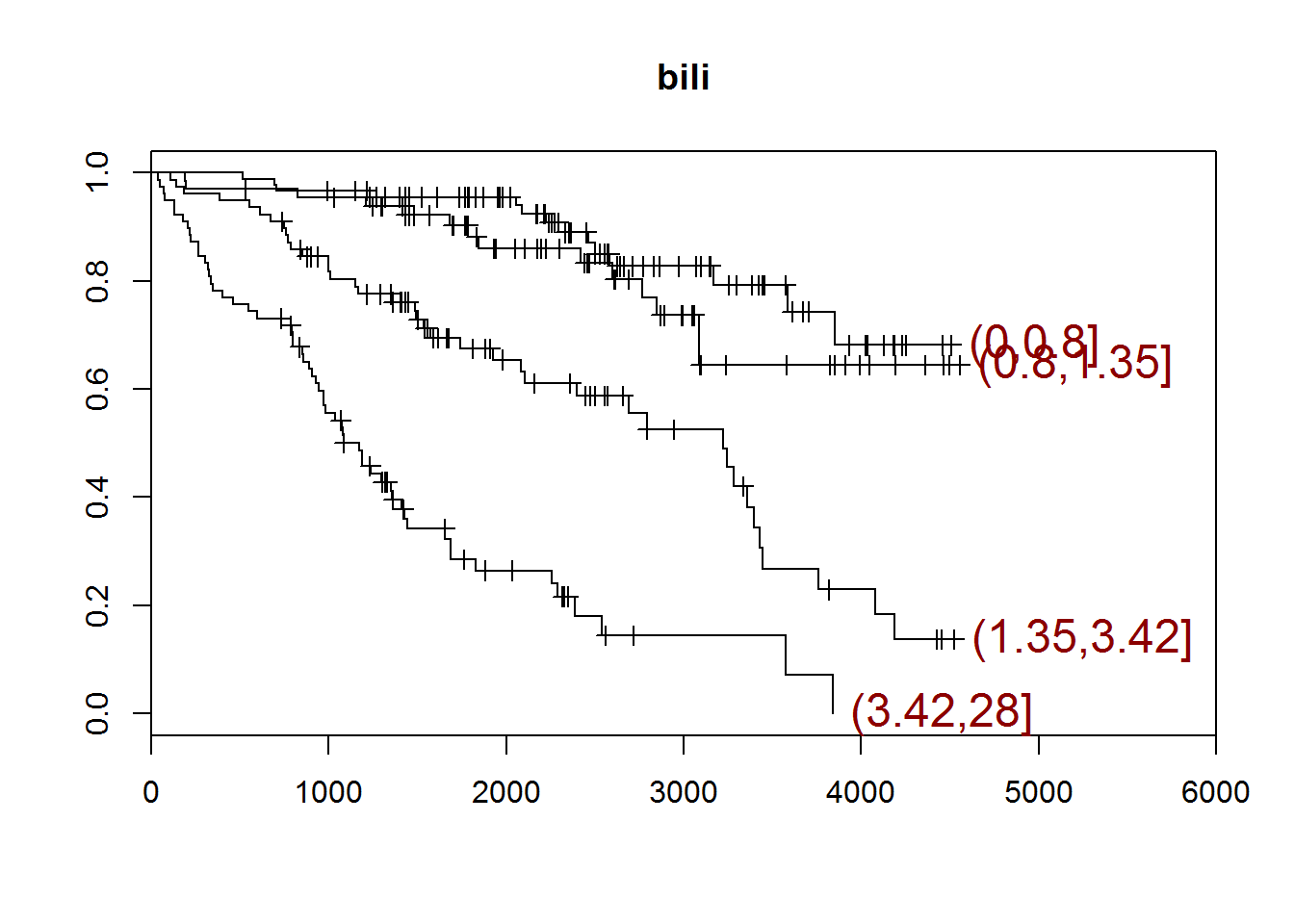
## [1] "chol"
## quartiles
## (0,250] (250,310] (310,400] (400,1.78e+03]
## 71 71 72 70
## [1] "There are 28 missing values."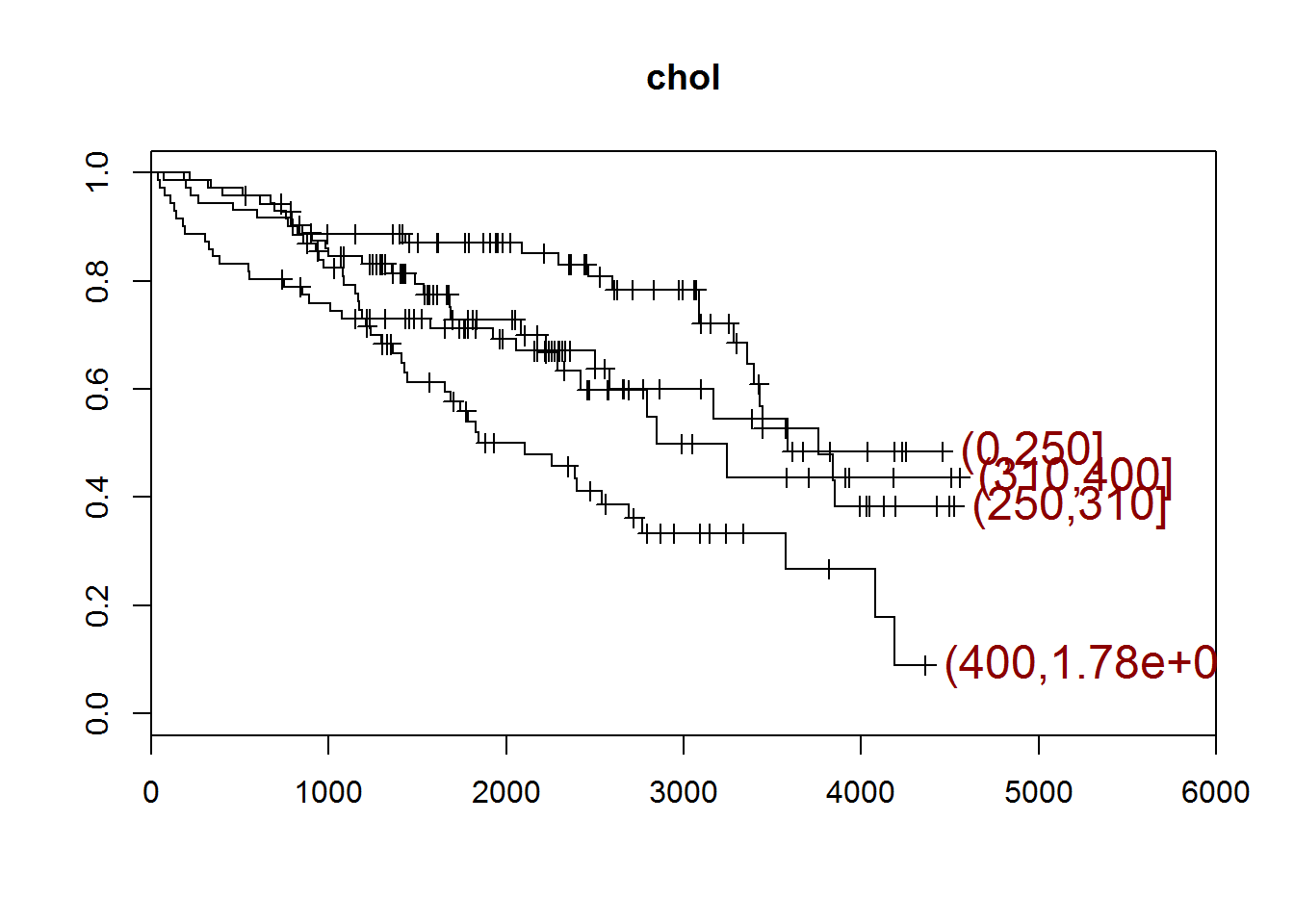
## [1] "albumin"
## quartiles
## (0,3.31] (3.31,3.55] (3.55,3.8] (3.8,4.64]
## 81 76 81 74
## [1] "There are 0 missing values."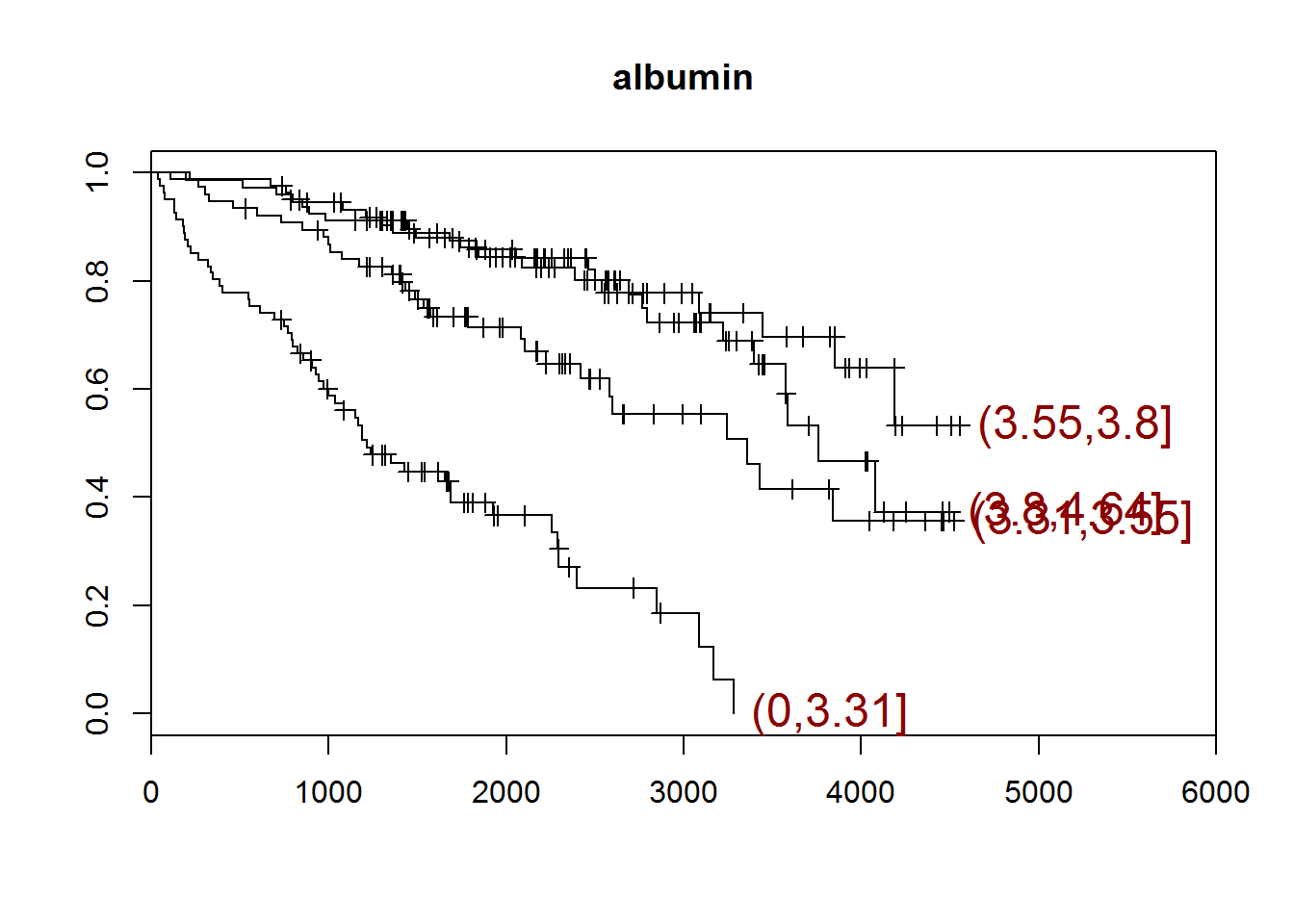
## [1] "copper"
## quartiles
## (0,41.2] (41.2,73] (73,123] (123,588]
## 78 80 75 77
## [1] "There are 2 missing values."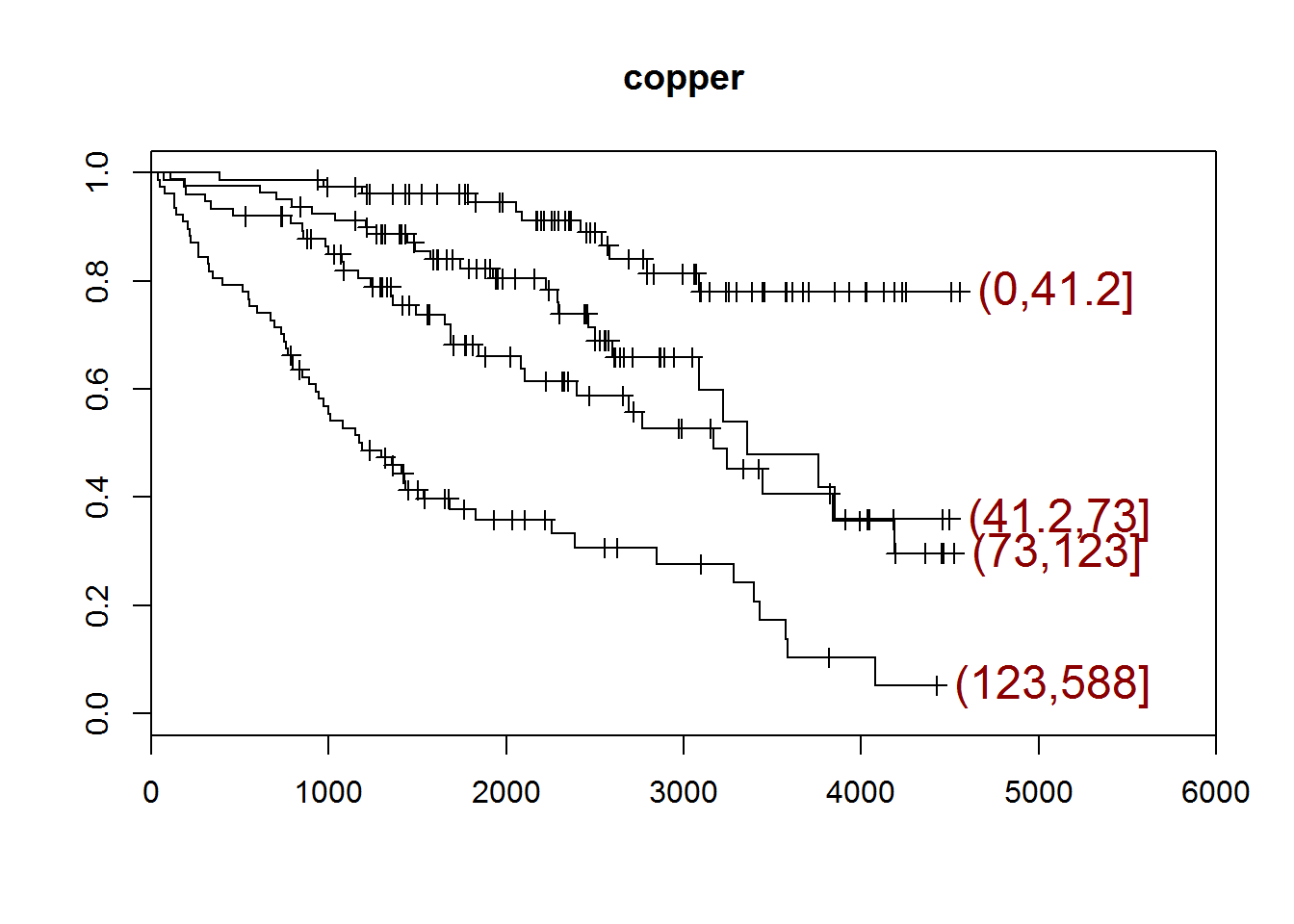
## [1] "alk.phos"
## quartiles
## (0,872] (872,1.26e+03] (1.26e+03,1.98e+03]
## 78 78 78
## (1.98e+03,1.39e+04]
## 78
## [1] "There are 0 missing values."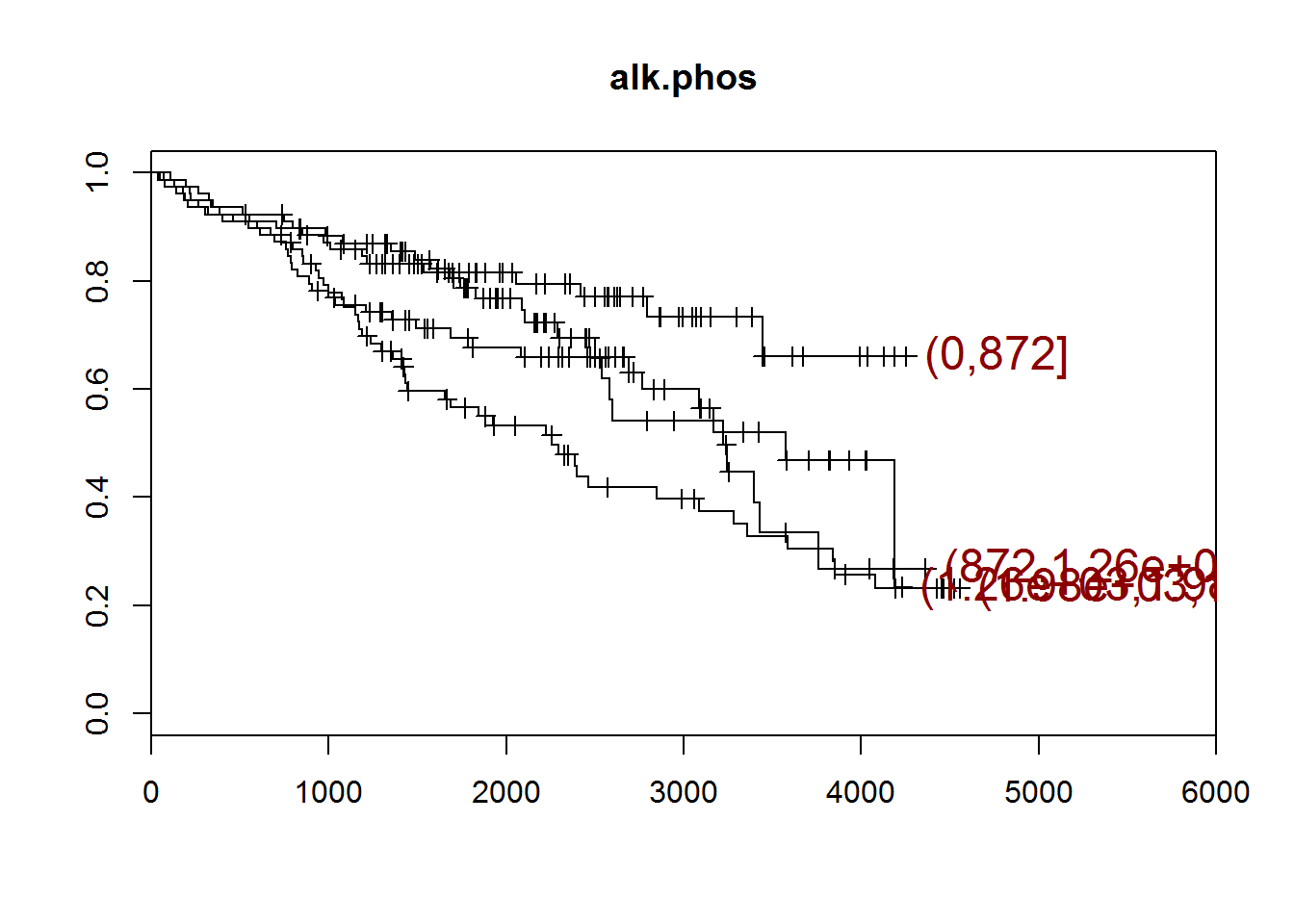
## [1] "ast"
## quartiles
## (0,80.6] (80.6,115] (115,152] (152,457]
## 79 78 79 76
## [1] "There are 0 missing values."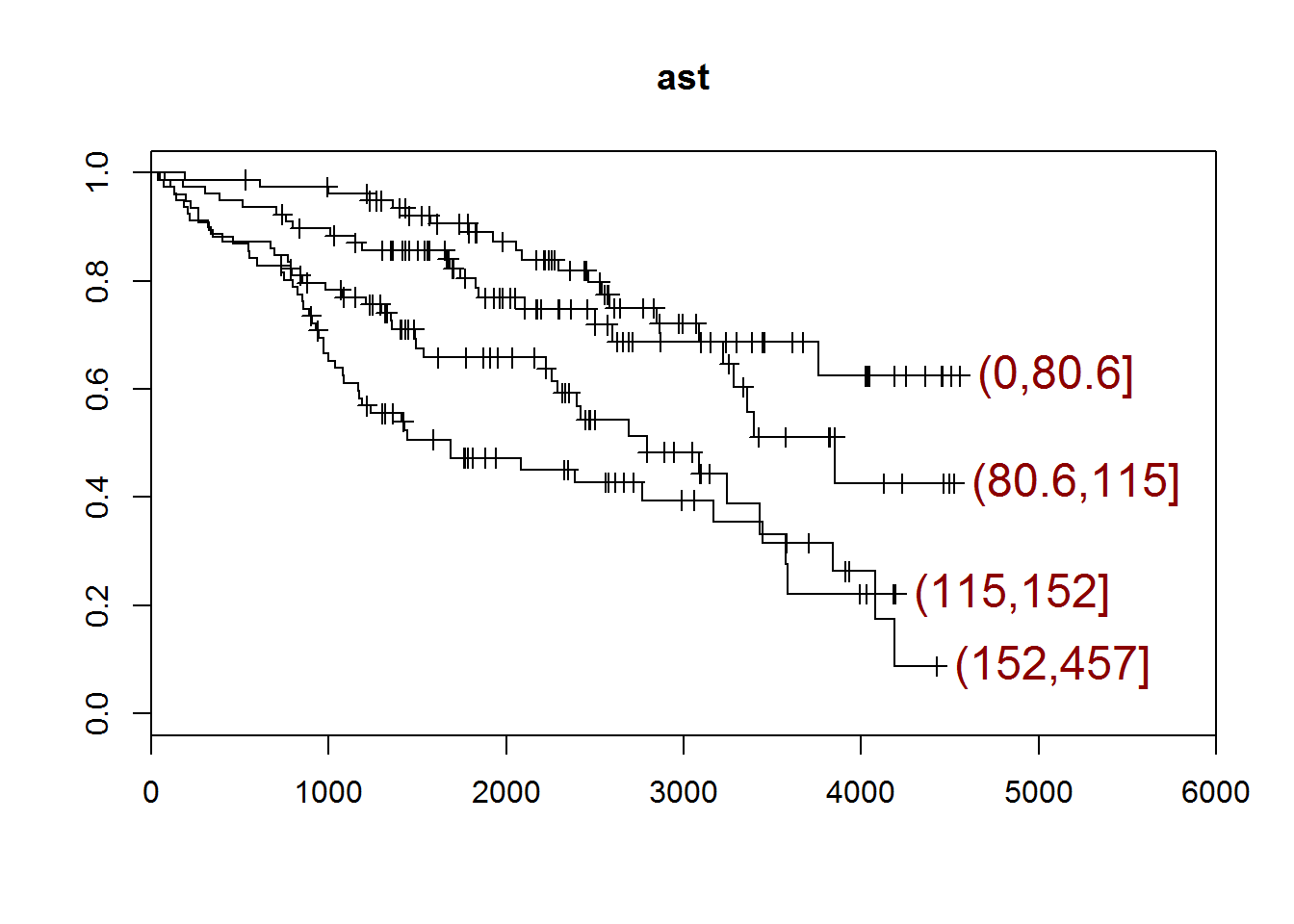
## [1] "trig"
## quartiles
## (0,84.2] (84.2,108] (108,151] (151,598]
## 71 71 70 70
## [1] "There are 30 missing values."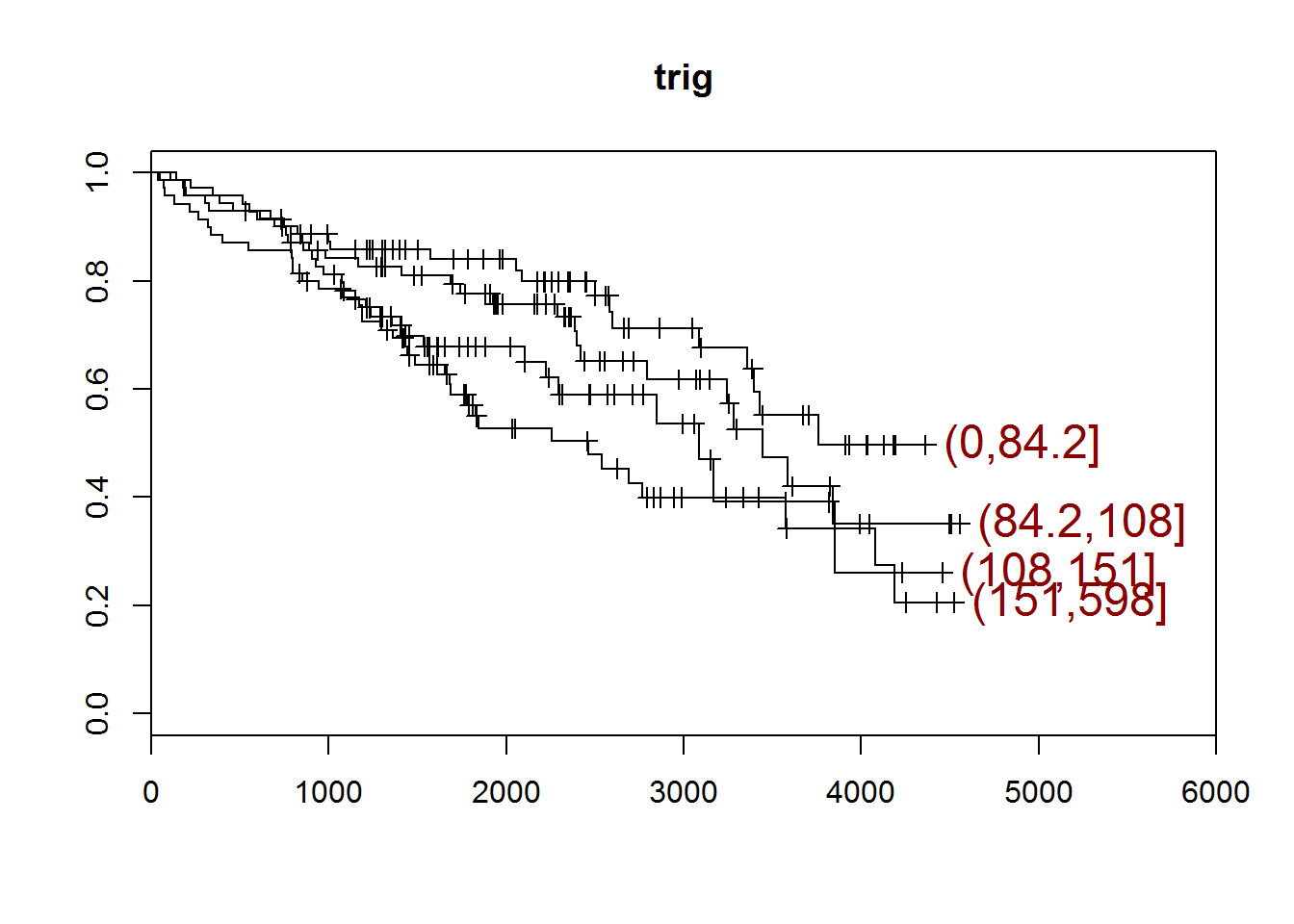
## [1] "platelet"
## quartiles
## (0,200] (200,257] (257,322] (322,563]
## 77 77 77 77
## [1] "There are 4 missing values."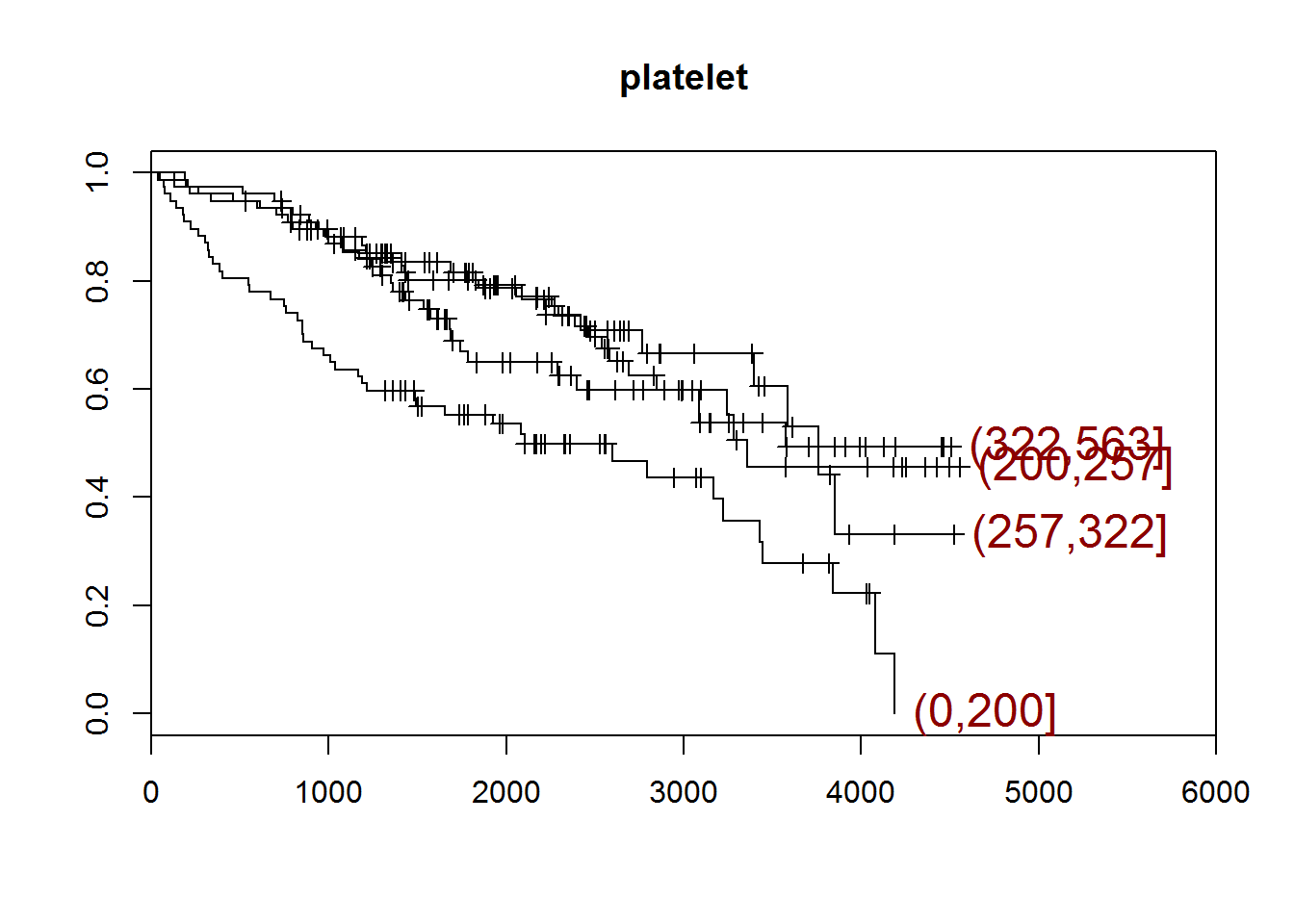
## [1] "protime"
## quartiles
## (0,10] (10,10.6] (10.6,11.1] (11.1,17.1]
## 89 85 61 77
## [1] "There are 0 missing values."