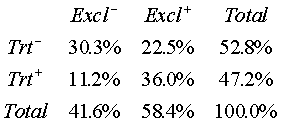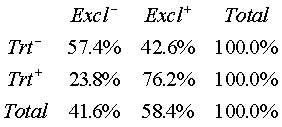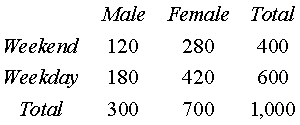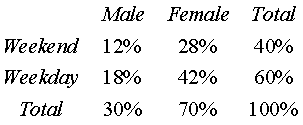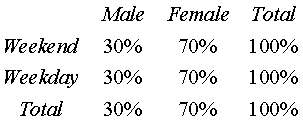StATS: What is independence?

Independence is a critical concept in Statistics. Two events are said to be independent if one event's occurence does not influence the probability that the other event will or will not occur.

Testing independence using cell probabilities.

Two events are independent if the probability of both events occuring together is equal to the product of the two individual probabilities.

In other words, is the probability in the cell equal to the product of the probabilities in the corresponding row and column totals.

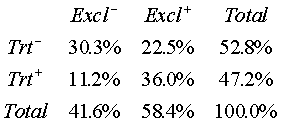
We can check this using the cell probabilities table. In the example shown above, the events NG Tube and Exclusive are NOT independent. The probability of NG Tube and Exclusive is 0.360. The product of the two individual probabilities is 0.584*0.472=0.2756.

Testing independence using conditional probabilities.

You can also test independence by checking to see if the conditional probability of an event is equal to the unconditional probability.

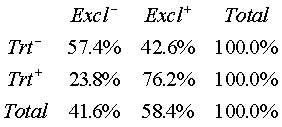
The table shown above has conditional probabilities for a breastfeeding study. The rows represet the control and treatment groups respectively. The columns represent bottle feeding and exclusive breastfeeding, respectively. The events NG Tube and Exclusive are NOT independent. The conditional probability,

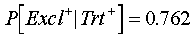
whereas the unconditional probability,

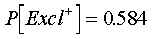
is much smaller.

In the following fictional example, visitors to the Emergency Room are classified as either arriving on a weekend or on a weekday. Further, visitors are classified according to gender.

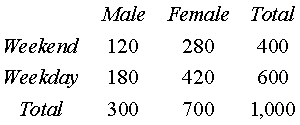
Shown above is the table of counts.

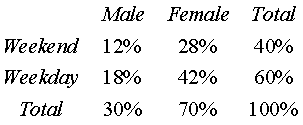
The events Male and Weekend are independent. The probability of both events occuring (0.120) and the product of the two individual events (0.300*0.400) are the same.

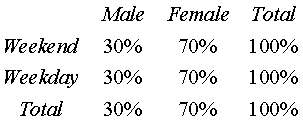
Another way of demonstrating this is noting that the conditional probability (0.300) is the same as the unconditional probability (0.300).

Deducing independence through logic.

In some situations, you can deduce independence without resorting to mathematics. If you can argue that it is impossible for one event to influence the probability of a second event, then the two events are logically independent.

Suppose, for example, that you randomly select two patients and watch them for development of a certain disease. If the patients are not related (i.e., no common genetic patterns) and if the disease is not infectious then the event that the first patient develops the disease is independent of the second patient developing the same disease.

Independence among several events.

The idea of independence can be extended to several events. Several events are said to be independent if the occurence of any one of the events does not affect the probability that the other events will occur.

If the events

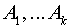
are independent events then the probability of all the events occuring simultaneously is the product of the individual proababilities. In other words,

If each of these independent events has the same probability (p), then the formula simplifies to

.

Example

In a study of chemotherapy for leukemia, we discover that of the 14 boys in the study, none showed evidence of abnormal testicular function.

If the 14 boys are independent and if the probability of developing abnormal testicular function after chemotherapy were 3% for each boy, what is the chance that we would see 0 out of 14 in our sample?

A probability of 3% is reasonably consistent with what we saw in the sample.

A variation on this example.

Suppose the probability of developing abnormal testicular function after chemotherapy were 30%?

This probability is much smaller. Under this assumption, it is unlikely to see no abnormal testicular function in a sample of 14 boys. A probability of 30% is not reasonably consistent with what we saw in the sample.

This page was written by Steve Simon while working at Children's Mercy Hospital. Although I do not hold the copyright for this material, I am reproducing it here as a service, as it is no longer available on the Children's Mercy Hospital website. Need more information? I have a page with general help resources. You can also browse for pages similar to this one at Category: Definitions, Category: Probability concepts.