[Previous issue] [Next issue]

Monthly Mean newsletter, January 2009

You are viewing the webpage version of the Monthly Mean newsletter for January 2009. This newsletter was sent out on January 18, 2009.

The monthly mean for January is 16.0.

Welcome to the Monthly Mean newsletter for January 2009. If you are having trouble reading this newsletter in your email system, please go to www.pmean.com/news/2009-01.html. If you are not yet subscribed to this newsletter, you can sign on at www.pmean.com/news. If you no longer wish to receive this newsletter, there is a link to unsubscribe at the bottom of this email. Here's a list of topics.

  1. Monthly Mean Quote.
  2. What is a boxplot?
  3. Crude versus adjusted comparisons.
  4. A false sense of frugality.
  5. Hide that randomization list.
  6. Monthly Mean Article: If we're so different, why do we keep overlapping? When 1 plus 1 doesn't make 2.
  7. Monthly Mean Blog: Health Care Renewal.
  8. Monthly Mean Book: The Survey Research Handbook. Guidelines and Strategies for Conducting a Survey.
  9. Monthly Mean Website: Regression with SAS Chapter 5: Additional coding systems for categorical variables in regression analysis.
  10. Nick News: Nick the rollerblader.
  11. Very bad joke: Two statisticians were traveling in an airplane from LA to New York.
  12. Tell me what you think.

1. Monthly Mean Quote.

Excellence in statistical graphics consists of complex ideas communicated with clarity, precision, and efficiency. Graphical displays should

Edward Tufte, The Visual Display of Quantitative Data, Second Edition, page 1. This excerpt summarizes Tufte's overall philosophy on design of statistical graphics. Dr. Tufte continued an outline of his design philosophy in two further books, Envisioning Information and Visual Explanations: Images and Quantities, Evidence and Narrative. I've read all of these books and highly recommend them. Dr. Tufte has a new book, Beautiful Evidence, that I have not read, but which has received mixed reviews. See commentary by National Public Radio, Yuri Engelhardt, and Stephen Few.

2. What is a boxplot?

The boxplot (sometimes called a box and whiskers plot) is a simple and very useful graphic display. I provided a nice definition of a boxplot at my old website. Other good explanations are at

The boxplot is useful for comparing the distributions of two different groups. If the median in one box exceeds the end of the box of the other group, that is evidence of a "large" discrepancy between the two groups. What passes as the median for one group would actually be the 25th or 75th percentile of the other group.

Just about any statistical software program (SAS, SPSS, Stata, R, etc.) can produce boxplots and you can find code to produce boxplots in many programming languages.

3. Crude versus adjusted comparisons

Many research papers describe crude versus adjusted comparisons. Here's an example:

This study was a secondary analysis of a randomized controlled trial of eradication of Helicobacter Pylori. The authors suspected that there may be an inverse relationship between blood pressure and stomach problems.

In 2003 we reported reduced stroke mortality among patients with oesophageal columnar epithelium (Barrett's oesophagus), with cerebrovascular deaths in patients with specialised intestinal metaplasia of the oesophagus being half that of the general population [1]. Subsequently, a postmarketing surveillance study of 18,000 patients on omeprazole in the United Kingdom has not shown any reduction in stroke mortality in these patients compared to the general population [2] but this drug is often prescribed for upper gastrointestinal conditions other than gastro-oesophageal reflux and Barrett's oesophagus. We hypothesised that the association we observed may be due to individuals with reduced lower oesophageal sphincter (LOS) pressure, (a risk factor for gastro-oesophageal reflux and Barrett's oesophagus) also having low vascular tone and blood pressure, resulting in reduced stroke risk. To investigate this, we examined whether blood pressure is associated with symptoms of gastro-oesophageal reflux.

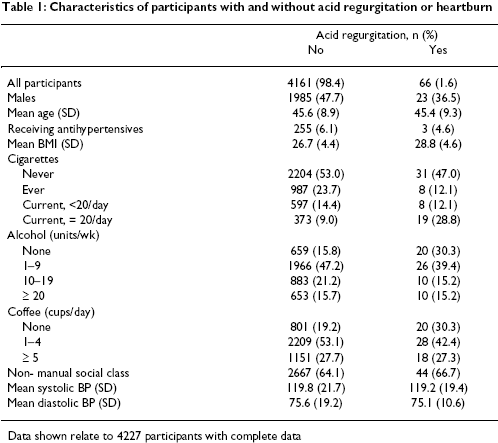
There were 4,227 patients eligible for the secondary analysis, with 107 and 66 experiencing daily heartburn or acid regurgitation, respectively. The average systolic/diastolic pressure was 119.8 / 75.6 for patients without acid regurgitation and 119.2 / 75.1 for patients with acid regurgitation. This difference was small, (0.6 / 0.5) but the comparison was not quite fair. The groups were not similar in their demographics. In particular, there was a large disparity in gender (48% males in the first group versus 36% males in the second group). There were also differences in lifestyle factors, with much less alcohol and coffee use in the acid regurgitation group. A portion of Table 1 is reproduced below.

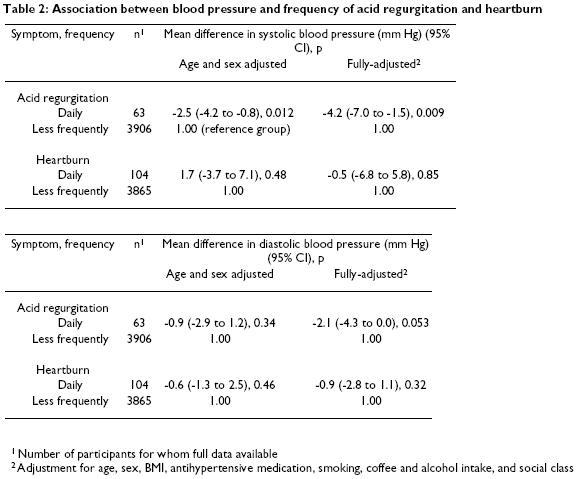
When you adjust for demographic and lifestyle factors, there is a 4.2 / 2.1 unit difference in systolic / diastolic blood pressure (see Table 2, reproduced after slight reformatting below).

How do these statistical adjustments work? In essence, you fit a regression model with both the treatment effect and all the relevant covariates. I describe the process in briefly in Chapter 1 of Statistical Evidence. The explanation given below is an adaptation and enhancement (as I am hoping with vain optimism that there might be a second edition of my book sometime in the future).

There is an interesting data file on Albuquerque housing prices at the Data and Story Library website. I have a nice description of the data set on my old website, and there is also a nice description at the DASL website.

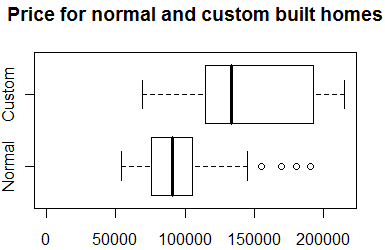
There is a large disparity between the prices of custom built homes and normal homes (see boxplot shown above). The average prices are 145 and 95 thousand dollars, respectively. Is this 50 thousand dollar disparity real, or can it be accounted for by other factors? One important factor is the size of the homes.

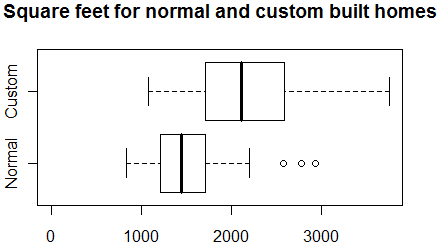
Not too surprisingly, custom built homes are a lot larger than normal homes (see boxplot shown above). The average sizes for custom built and normal homes are 2,100 and 1,500 square feet, respectively. Could the 50 thousand dollar difference in price be accounted for solely by the difference in sizes? A multiple linear regression model can help us answer this question.

The model evaluating the effect of custom build on price without any information about square footage (see below) has an intercept of 94,752 and a coefficient associated with the indicator variable for custom build (cust) of 49,926. The intercept tells you that the estimated average price of normal houses is 95 thousand dollars. The custom build term tells you that the estimated average change in price when you switch from a normal house to a custom built house is 50 thousand dollars.

When you include the size of the house (sqft) in the regression model (see below), the coefficient for custom build is reduced to 14,285.99. This tells you that there is indeed a difference in price between custom built and normal homes, but it is only 14 thousand dollars, not nearly as large as the crude comparison might lead you to believe.

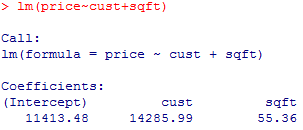
Notice that the slope for sqft is 55.36, which tells you that each additional square foot adds about 55 dollars to the price of either a normal or a custom built house. There was originally a discrepancy of about 650 square feet in the sizes of the two types of homes. This tells you that approximately 36 thousand dollars ( = 55 * 650, approximately after rounding) dollars of the difference in average price between custom built and normal houses can be accounted for by the difference in sizes. Thus 14 ( = 50 - 36) thousand dollars of the difference in price remains after adjusting for house size.

There's another way to look at this adjustment. Place a trend line through the average square footage and average sales price of regular homes. The trend line should have a slope equal to 55.

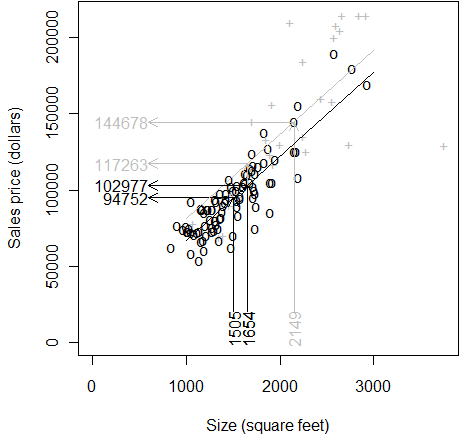
I am using gray in this graph to temporarily de-emphasize the custom build data. Now if you project the price for a regular home at 1,505 (the average size of all regular homes) you would get an unadjusted mean price of 94,752. What would we project the sales price to be, however, if the size were 1,654 (the average size of all homes, both regular and custom built)? It would have to be higher, of course. The sales price when you adjust the size upward is 102,977. Note that when you increase the size by about 150 square feet, you get an increase of about 8 thousand (approximately 150*55, but I am rounding a bit for simplicity).

Place a similar trend line in place for the custom built homes. The trend line has a slope of 55 again and it goes through the mean square footage and mean size for custom built homes only. This trend line is higher than the previous trend line because of the location of the means are different.

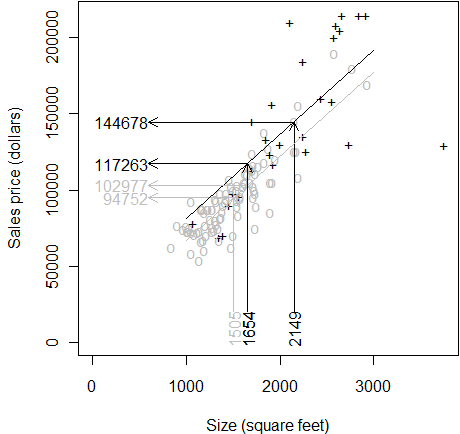
If you project the price for a custom built home at 2,149 (the average size of all custom built homes) you get the unadjusted mean price of 144,678. What would the price be if we adjusted the size downward to 1,654? It's 117,263 which is lower, or course. When the size of the house decreases by about 500 square feet, the price is adjusted downward by about 27,500 (=500*55).

The bottom line is that there is about a 50 thousand dollar discrepancy in price between custom built and normal homes, but after you account for the differing sizes of custom built and regular homes, the discrepancy decreases to about 14 thousand dollars. Thus, about 70% of the difference in prices can be accounted for by the difference in average sizes.

Going back to the example with adjustments for systolic and diastolic blood pressure, the concept is the same, but you can't display the data graphically because there are too many variables. You fit a multiple linear regression model with systolic or diastolic blood pressure as the dependent variable. Then you include an indicator variable for acid regurgitation and all the covariates (age, sex, bmi, antihypertensive medication, smoking, coffee, and alcohol intake, and social class). Get a predicted value for acid regurgitation at the overall average values of the covariates and compare it to the predicted value for no acid regurgitation at the overall average values of the covariates.

4. A false sense of frugality

A while back I received a data set that was very well documented, but there was one thing that I wish that the data entry person had not done. The demographic data was listed as 45f, 52m, 22m, 21f, etc. This was obvious shorthand for a 45 year old female, 52 year old male, and so forth.

When you squeeze both pieces of information into the same cell, you lose the ability to compute simple statistics. Most statistical software programs, for example will not know to drop the last letter before computing the average age, or to ignore the first two digits when computing the percentages of males and females.

I explain what Microsoft Excel functions I used to split this information into two separate cells at www.pmean/08/FalseFrugality.html. I also offer five fundamental rules of data entry on my old website at www.childrens-mercy.org/stats/data/entry.asp.

This is not the first time that I have encountered someone who wants to squeeze two pieces of information in the same cell. A common problem is when a data entry person records blood pressure as 120/60. This is a problem for two reasons. First, it is impossible to compute an average of either the systolic or diastolic blood pressure when the data is recorded like this. Second, some systems may misinterpret 120/60 as a division and produce a value of 2.

Another researcher decided to use ID values of 1A, 2A, 3A, ..., 25A followed by 1B, 2B, ..., 25B. This was not a terrible thing in itself, but nowhere other than the last character of the ID was it apparent which observations belonged to group A and which belonged to group B. This means that there is no easy way to calculate statistics just on group A or group B. It would have been simpler to label the ID values as 1 through 50 and include As and Bs in a separate column.

5. Hide that randomization list

One of the many things I learned from Evidence-Based Medicine is the importance of concealed allocation. That's a fancy term for "hide that randomization list." Why you need to hide the randomization list says a lot about research practice and the problem with ethical conduct during a clinical trial.

In a randomized trial, it is effectively the flip of a coin that decides what therapy each volunteer patient in the trial gets. The patient willingly cedes authority of the choice of medical therapy. The amazing thing is that the patient cedes this choice not to a trusted authority like his/her doctor, but rather to a totally random device. This makes the conduct of a clinical trial quite different than the process in which health care is normally delivered. In a normal clinical setting, the patient and doctor will discuss the various treatment options and reach a mutually agreeable course of action.

Patients can subvert the randomization process if they wish. For example, if a patient is randomly allocated to a surgical arm of a study, he or she is perfectly within their rights to "chicken out" after the study starts and ask for a non-surgical intervention instead. Principles for the ethical conduct of research established during the Nuremberg trials require that patients be allowed to withdraw from a research study at any time.

The patient's doctor has an obligation in a clinical trial to let the patient know what treatment options are (in the doctor's opinion) best for the patient. If a doctor has a reasonable belief that one of the therapies being offered in a clinical trial is not in the best interests of the patient, that doctor should advise the patient not to enter the trial. If there is a 50% chance at getting an inferior therapy by participating in a clinical trial, then you have to explore treatment options outside the research study.

The key concept in this is equipoise, a genuine uncertainty about which treatment is better. If a doctor has more than just a hunch that one arm of the trial is superior for all patients, he/she cannot participate in the trial. If the doctor has more than a hunch that one arm of the trial is superior for this particular patient, that doctor can still refer other patients to the trial, but not this particular patient.

Sometimes doctors will try to subvert the randomization process. They encourage their patients to participate in the trial, but they try to steer some or all of their patients into a particular arm of the study. There are several reasons they might do this.

Perhaps the doctor is trying to earn more money through the recruiting bonuses in a trial. If the recruiting bonuses are so large as to encourage this sort of behavior, then part of the problem lies with the researcher who set up these financial incentives.

Another possible motive would appear if a certain therapy was available only through the clinical trial. This happens a lot, and the ethical question raised is whether society has the right to withhold a promising therapy from patients who are unwilling or unable to participate in a randomized trial. There is a societal imperative to insure that therapies are tested in a rigorous setting before they are made generally available to all patients, but it is unclear (at least to me) whether this societal responsibility trumps the individual patient's needs.

A third motivation might be a desire to protect the patient. If, for example, one therapy in a study is thought to be possibly better, but possibly with harsher side effects, doctors might be tempted to steer their weaker patients away from this therapy. This can happen in very subtle and possibly even subconscious ways. For example, an older frailer patient wants to enter the clinical trial, and you know that he/she will be assigned to the more toxic but potentially more efficacious drug. You might interpret the inclusion criteria quite carefully and cautiously. If the less toxic drug were the one waiting for assignment to that incoming patient, you might be a little more lax in your interpretation of the inclusion criteria.

This last motivation might seem to be in the patient's best interest, but even if it is, it totally destroys the scientific integrity of the research study. The weak and frail patients are more likely to be excluded from one arm of the study than the other.

It is really important, therefore, that you hide the randomization list from the physicians who are recruiting patients into a study until after the patient and doctor both agree that it is in the patient's best interest to be part of the study. One way to do this is to give the doctor a series of sealed envelopes. Only after there is agreement to participate in the randomized trial is the envelope opened, revealing which therapy the patient is randomly assigned to.

Envelopes will prevent subconscious bias in the application of inclusion criteria, but there is nothing to prevent a determined physician from peeking in the envelopes ahead of time and then arranging for a given patient to be entered into the study when the preferred envelope is due to be opened.

Better protection against peeking is the use of an 800 number for recruitment. If a doctor and patient agree to be part of the study, then they call an 800 number and talk to a centralized operator who takes down all the relevant information and then provides the treatment allocation over the phone.

Concealed allocation is very important for many studies, but it doesn't make sense in some situations.

First, and most obviously, you can only hide the randomization list only if the study is truly randomized. Observational studies do not try to allocate therapies as part of the research process, so concealed allocation is a non sequitur.

Second, in a blinded study, the randomization list is already hidden from everybody except the person in the back of the pharmacy who prepares the pill packages. So a blinded study would automatically have concealed allocation.

Finally, in a small study where the principal investigator is also the person who does all the recruiting, concealed allocation is overkill. You can presume that the person who designed the study would not try to subvert the study.

I hope to elaborate on this topic in greater detail on my website soon. I want to discuss some of the empirical evidence that has been published about this problem. I also want to describe an excellent book on this topic, Berger V. Selection Bias and Covariate Imbalances in Randomized Clinical Trials. 1st ed. Wiley; 2005, but I have to read the book first!

6. Monthly Mean Article: If we're so different, why do we keep overlapping? When 1 plus 1 doesn't make 2.

Wolfe R, Hanley J. If we're so different, why do we keep overlapping? When 1 plus 1 doesn't make 2. CMAJ. 2002;166(1):65-66. Available at: http://www.cmaj.ca/cgi/content/full/166/1/65 [Accessed January 5, 2009].

You've all seen graphs like this one (I removed some identifying information to preserve privacy).

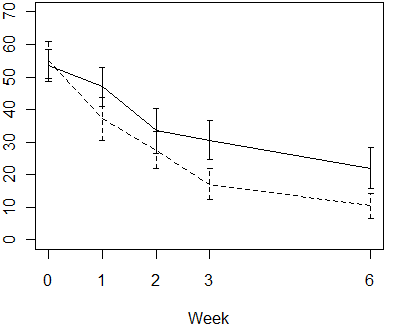
In this graph, the error bars represent 95% confidence intervals for the individual means. When the intervals don't overlap, as they do at week 3 and 6, that is a safe indication that there is a statistically significant difference between the averages of the two groups. But what about the other weeks. If the confidence intervals overlap, but only by a little bit, then it is still possible that there may be a statistically significant difference between the two means. The article by Wolfe and Hanley explains why this happens.

7. Monthly Mean Blog: Health Care Renewal, Bernard Carroll, Cetona, Roy M. Poses MD, MedInformaticsMD, Wally R. Smith, MD, wiswal, APeticola, Kimball Atwood MD. hcrenewal.blogspot.com

The Health Care Renewal blog is is dedicated to "addressing threats to health care's core values, especially those stemming from concentration and abuse of power." Note that some of the authors use their real names and others use pseudonyms. A large portion of this blog is devoted to abuses of the research enterprise. The blog entries that discuss these issues are, for the most part, labeled with one of the following categories: conflicts of interest, evidence-based medicine, manipulating clinical research, pseudo-evidence based medicine, suppression of medical research, and/or transparency. 

8. Monthly Mean Book: The Survey Research Handbook. Guidelines and Strategies for Conducting a Survey

The Survey Research Handbook. Guidelines and Strategies for Conducting a Survey. Pamela L. Alreck, Settle, Robert B. (1995) Chicago, IL: Irwin Professional Publishing. Description: A very practical reference on surveys with a lot of emphasis on planning. There are useful guidelines and checklists throughout the book. It is an excellent book for beginners because there are very few mathematical formulas.

9. Monthly Mean Website: Regression with SAS Chapter 5: Additional coding systems for categorical variables in regression analysis, Xiao Chen, Phil Ender, Michael Mitchell and Christine Wells.

When you have a categorical variable with k levels in a regression model, you can replace it with (k-1) indicator variables. For example, if your categorical variable has five levels: A, B, C, D, and E, then the four indicator variables would be I1 = 1 if category A and 0 otherwise, I2= 1 if category B and 0 otherwise, I3 = 1 if category C and 0 otherwise, and I4 = 1 if category D and 0 otherwise. The resulting coefficients represent the estimated mean of the level being indicated by 1 minus the estimated mean of the level not coded by any of the indicator variables (usually the last level). For example, the coefficient associated with I1 would be the estimated mean for level A minus the estimated mean for level E.

There may be times, however, where you want to use a different coding scheme. For example, forward difference coding would have I1 = 1 if level B, -1 if level A, and 0 otherwise; I2 =1 if level C, -1 if level B and 0 otherwise; and so forth. The interpretation of the regression coefficients for this coding scheme, is quite surprisingly different from what you'd expect. The coefficient for I1 would be the mean for level A minus the mean for levels B through E.  The coefficient for I2 would be the mean for levels A and B minus the mean for levels C through E. The coefficient for I3 would be the mean for levels A through C minus the mean for levels D and E. The coefficient for I4 would be the mean for levels A through D minus the mean for level E. One explanation for the counterintuitive interpretation is that the estimated slope coefficient in a multiple linear regression model is only sensible if the other variables are held constant.

I have never found a good source for the variety of ways that you can code a categorical variable until I ran across this website. It explains how to set up the following systems.

The examples all use SAS, as you might have predicted from the title of the webpage. Still, these methods can easily be adapted to other statistical software programs. URL: www.ats.ucla.edu/stat/sas/webbooks/reg/chapter5/sasreg5.htm

10. Nick News: Nick the roller blader

During Christmas break, students at Nicholas's school were given a coupon for a free admission to a roller skating session at Skate City. Nicholas loves skating (meaning roller blades, not ice skating). We both took him on December 30, but Steve, having done skating with Nicholas before, wisely decided to let Nicholas do all the skating and he'd do the watching. It's not that I fall down less than Nicholas does, it's that when I fall, it is farther to the ground, and my weight produces greater momentum. Nicholas just picks himself back up and keeps going. Cathy had skated a lot as a child, so she rented some skates to go out with Nicholas. You can imagine how this turned out, but you can find the full story and a picture of Nicholas at

11. Very bad joke: Two statisticians were traveling in an airplane from LA to New York

This story is found at the R.A. Fisher Hall (joke #24) of the Gary Ramseyer's Internet Gallery of Statistics Jokes, and it shows the true meaning of the term "dangerous extrapolation." I use this joke at the start of my class on regression analysis.

Two statisticians were traveling in an airplane from LA to New York. About an hour into the flight, the pilot announced that they had lost an engine, but don't worry, there are three left. However, instead of 5 hours it would take 7 hours to get to New York. A little later, he announced that a second engine failed, and they still had two left, but it would take 10 hours to get to New York. Somewhat later, the pilot again came on the intercom and announced that a third engine had died. Never fear, he announced, because the plane could fly on a single engine. However, it would now take 18 hours to get to New York. At this point, one statistician turned to the other and said, "Gee, I hope we don't lose that last engine, or we'll be up here forever!"

12. Tell me what you think.

How did you like this newsletter? I have three short open ended questions that I'd like to ask. It's totally optional on your part. Your responses will be kept anonymous, and will only be used to help improve future versions of this newsletter.

I only received feedback from two people (that's okay, since feedback is totally optional). One person had an interesting take on my newsletter.

I don't think I read your newsletter to learn specific things as much as to be reminded of a way of thinking. I see so much use of statistics that I suspect is really lousy that it is useful to just immerse myself in the words of someone who knows what he's talking about, loves the field, and is able to teach/communicate well. I think I read your newsletter for inspiration ... for the fact that it returns me to a place of clarity and dare I say hope??

I'm not sure I always know what I'm talking about, but I do try to get people to think about how statistics are used in the real world. You don't have to be a rocket scientist or a brain surgeon to be able to critically evaluate the use of statistics in the real world. If one person finds this inspiring, then I'm happy.

Another respondent liked my discussion on overfitting, but found my discussion on combining measures on different scales of measurement confusing. I'll see if I can clarify the latter point in a future webpage or newsletter entry.

Both respondents had interesting suggestions for future discussion.

One suggestion was about the use of propensity score, and whether it should used as a matching factor, a weighting factor, or a categorizing factor. This is something I am actively working on for a client, and I hope to put some of this up soon.

Another suggestion was an explanation of adjusted odds ratios in logistic regression. I have some material on this at my old website and I'll try to elaborate further on this.

A third suggestion was for "basic statistics" although there was some concern that this might be boring for other readers. I generally have found that people who are interested in help will invariably use the term "statistics for beginners." Actually, they will use a more perjorative term like "idiots" or "complete dummies" but this is not true. The people who ask for help are almost always very well educated and well read. They just lack experience in a particular area that I happen to know a few things about. In all the classes I've taught recently and all the webpages I've written, I've only received one request to make the discussion more technical. Even in people who I recognize understand statistics well, their desire is still for more basic information. I'm all in favor of getting a more solid understanding of the fundamentals.

A final request came in more of the form of a complaint. In some studies, a single patient may have more than one procedure. This can lead to some confusing situations and the researchers themselves often fail to distinguish between patients and procedures. I think it is critical to always know how much data you have and of what type. The classic example that I encountered was a breastfeeding study with a data set of  84 infants born to 72 mothers because 12 of the mothers had given birth to twins. I'll try to write up something about this and about a closely related topic, pseudo-replication, for a future newsletter.

What now?

Sign up for the Monthly Mean newsletter

Review the archive of Monthly Mean newsletters

Go to the main page of the P.Mean website

Get help

Creative Commons License This work is licensed under a Creative Commons Attribution 3.0 United States License. This page was written by Steve Simon and was last modified on 2017-06-15. Need more information? I have a page with general help resources. You can also browse for pages similar to this one at Category: Website details.