[The Monthly Mean] February 2009--What IRBs should look for in a data safety and monitoring plan (released 2009-02-23)

Monthly Mean newsletter, February 2009

The monthly mean for February is 14.5. This is the lowest value in 24 months.

Welcome to the Monthly Mean newsletter for February 2009. This newsletter was sent out on February 23, 2009. If you are having trouble reading this newsletter in your email system, please go to www.pmean.com/news/2009-02.html. If you are not yet subscribed to this newsletter, you can sign on at www.pmean.com/news. If you no longer wish to receive this newsletter, there is a link to unsubscribe at the bottom of this email. Here's a list of topics.

What IRBs should look for in a data safety and monitoring plan.

A simple improvement to the binomial confidence interval.

Is there a sample size too small to allow efficient randomization?

Monthly Mean Article: The challenges faced in the design, conduct and analysis of surgical RCTs.

Monthly Mean Blog: The Ask Edward Tufte Forum.

Monthly Mean Book: How to Report Statistics in Medicine.

Monthly Mean Definition: What is a percentile?

Monthly Mean Quote: If your experiment needs statistics,...

Monthly Mean Website: Statistical Problems to Document and to Avoid

Nick News: Nick the traveler, part 1.

Very bad joke: Face it-I'm your statistically significant other.

Tell me what you think.

1. What IRBs should look for in a data safety and monitoring plan.

The process that a data safety and monitoring board (DSMB) follows can appear intimidating to the average researcher and to the average member of an Institutional Review Board (IRB). It is indeed a complex process for a committee to review an ongoing research study and make an intelligent determination about whether the study should continue or if it should end early. There is a complex dynamic involving the protection of the interest of the individual research subjects in the study and the preservation of the scientific integrity of the research protocol. If you are asked to review a protocol that involves a DSMB, you shouldn't tinker with the details, but there are some broad issues that you should feel free to comment on.

The first issue is whether a DSMB is needed at all. There is no hard and fast rule about this. Granting agencies are becoming more likely to insist on a DSMB for more of the research they are funding, and that is clearly a mandate you can't ignore. In other situations, however, you should ask whether a simpler structure may be more appropriate.

Perhaps the principal investigator, by himself/herself or in combination with other members of the research team could serve the same function as the DSMB. The protocol would then list specific situations where the PI would be allowed to end the study early and situations where the PI would be forced to end the study early. It would almost certainly be appropriate to add a condition along the lines of "New information may emerge during the trial, either from the trial data itself or from newly published research relating to the medical condition being studied. If this information, in the opinion of the PI, adversely affect the cost/benefit balance for patients entering the study, then the study should stop enrolling patients." Nothing in this statement, of course, would prevent or discourage an IRB from ending a study if it saw evidence during the continuing review of a study that adversely upset the cost/benefit balance.

Demand an independent DSMB if the PI has a financial stake in the results of the study. Almost all phase III studies conducted by Pharmaceutical firms use a DSMB for this reason. A DSMB is also called for if the design of the research study is very complex, such as the use of multiple sites. Finally DSMBs are needed when the stakes are high, such as in treating a life threatening disease.

If the IRB determines that a DSMB is needed, then they should insist that the DSMB must develop guidelines for early stopping prior to data collection. The guidelines, however, should be sufficiently flexible to allow the DSMB to take action in the event of unexpected findings during the conduct of the study. You always need an escape clause if a drug to prevent hair loss suddenly turns every patient into a werewolf, even if there was no reason to suspect lycanthropy as a side effect at the start of the study. Still, the DSMB should spell out as much as possible in advance.

Any decision to end a study early should explain how this affects patients in the middle of the study. In some studies, stopping early also means stopping the therapy of any currently enrolled patients in midstream. In other studies this is the worst thing you could do and a a phased ending of the therapy might be needed. Possibly, the only change would involve patients getting the placebo being notified of their status with the recommendation that they switch to the active therapy. Sometimes nothing should be done until the currently enrolled patients complete all of their evaluations.

The IRB should ask how patients who have completed the trial should be notified if a study is stopped early for safety reasons. These patients are no longer at risk because they have stopped taking the therapy required in the research study, but the simple principle of respect would demand that they be kept informed of any issues serious enough to cause the study to stop early. Notification to these patients might include recommendations about additional tests or health monitoring.

Insist that standards for stopping early for safety reasons not be held to as high a statistical standard as stopping early for efficacy reasons. There is an extensive literature on the chances for declaring a false positive result when you evaluate the data at multiple time points. I myself show some simple results along these lines at my old website.

The statistical adjustments for these situations are complex, and the IRB should not be expected to understand all the nuances of these methods. The IRB, however, should make sure that safety issues are not held to the same rigorous standard as early evidence of efficacy. The reason for this is that stopping early for safety reasons does not raise the same issues about false positive findings. This is not to say that stopping early for safety reasons should be done without statistical rigor. Rather, it is just an acknowledgment that safety is different. A DSMB, for example, should not mindlessly apply a Bonferroni correction to multiple safety outcomes. A DSMB should examine deviations in safety endpoints both with respect to the control group and with respect to historical norms. While some efficacy endpoints can be evaluated without breaking the blind, the DSMB should always have access to unblinded safety data.

Finally, make sure that the people on your IRB responsible for continuing review have access to any reports produced by the DSMB. Information produced by the DSMB should be very helpful in deciding whether a consent form needs to be modified or if the cost/benefit balance has been altered. You should not rely solely on the DSMB, of course, but they will provide you will lots of useful data. This may be a touchy point with some researchers. A DSMB report showing a trial that is just on the verge of stopping could, if made public, dry up the patient pool just a few weeks or months before declaring victory. Although some people have advocated that patients enrolling in a trial cannot have truly informed consent without having access to all the data collected up to that point, such disclosure can cause serious trouble with the research. Thus, the IRB should respect the confidentiality of the DSMB report.

2. A simple improvement to the binomial confidence interval.

The traditional formula for a confidence interval for a proportion fails to work well when the sample proportion is very close to zero or very close to one. I won't show the formula here, but the traditional formula involves adding and subtracting a certain amount from the sample proportion. Adding and subtracting the same amount makes the interval symmetric. The figure below illustrates these intervals.

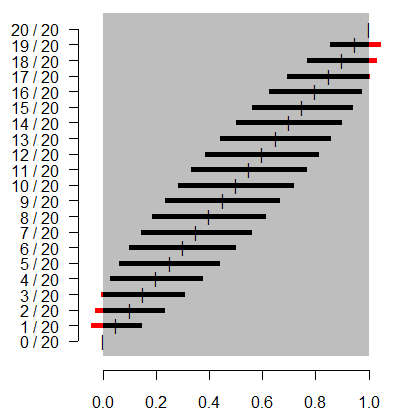
This figure shows what a traditional confidence interval would look like when you observed 0 events out of 20, 1 event out of 20, etc. Notice that for extreme proportions such as 1/20 and 19/20, the confidence limit extends well outside the permissible range for a probability. Symmetry is not a good property to have. The traditional interval has additional issues at the most extreme cases (0/20 and 20/20). There the interval has zero width, which we know is not correct. There are some adaptations that work better than the traditional confidence interval. The Wilson interval, for example, is shown below.

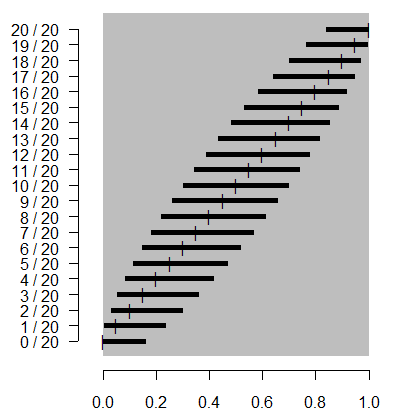
Again, I won't show the formula here, but notice that the interval is highly asymmetric for proportions close to zero or close to 1. For the cases 0/20 and 20/20, the interval is as asymmetric as you can get with the sample proportion sitting right on top of one of the confidence limits. If you're someone who likes staring out formulas, you will notice that at a 95% confidence level, the formula for the Wilson interval is not too much different than the traditional interval with 2 added to the numerator of the sample proportion and 4 added to the denominator. If you're someone who doesn't like staring at formulas, just trust me on this. The graph below shows how the approximation looks.

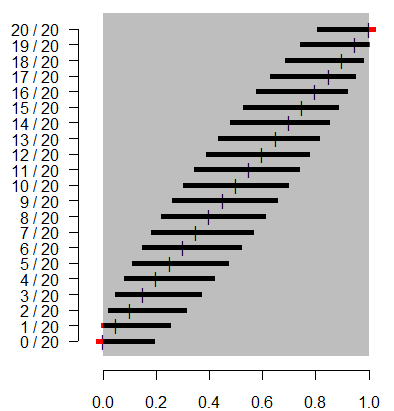
It's not perfect. The extreme cases of 0/20 and 20/20 still extend too far outside the permissible range for probabilities, but at least this approximation provides an interval with width greater than 0. Adding 2 and 4 to the numerator and denominator effectively pushes the interval inward. It creates an asymmetry where the limit closer to 0 or 1 is shrunk and the limit closer to the middle is expanded. For proportions that are not extremely close to 0 or 1, the net effect of adding 2 and 4 to the numerator and denominator is small.

There are many ad hoc rules about how to handle extreme proportions, such as adding/subtracting 0.5/n. The nice thing about adding 2 and 4 to the numerator and denominator is that it is easy to do and it draws support from a theoretical perspective.

If you want to see the formulas, there is a Wikipedia article on the binomial proportion confidence interval that I myself made some contributions to.

3. Is there a sample size too small to allow efficient randomization?

Randomization is the process of selecting the therapy that a patient receives in a clinical trial using a random device like a flip of a coin, a roll of a die, or (most frequently) a random number generator on a computer. Randomization helps assure that the both therapies in a clinical trial get roughly the same mix of good prognosis and poor prognosis patients. It relies on the law of large numbers. But what's large? Louis Hsu tackled this problem in a study published in 1989.

Hsu LM. Random sampling, randomization, and equivalence of contrasted groups in psychotherapy outcome research. J Consult Clin Psychol. 1989;57(1):131-7.

He considered cases where there were one, two, or three potential binary confounding variables and considered randomization to be a failure if the proportions for any confounding variable was twice as large in one group as in the other. As expected, with small sample sizes, the chances are good that you would still have a large imbalance in a potential confounding variable. If, however, you have 40 observations per group, then even with three potential confounding variables, there is only a small probability of finding a large imbalance in one of these potential confounders. If the number of potential confounders is small, then perhaps a sample size of 20 observations per group would be acceptable.

What do you do if you're randomizing, and you only have 10 observations per group? You should consider matching or stratification of the randomized sample. An interesting and underutilized alternative to randomization is minimization.

Treasure T, MacRae KD. Minimisation: the platinum standard for trials? BMJ. 1998;317(7155):362-363. Available at: http://www.bmj.com/cgi/content/full/317/7155/362 [Accessed February 18, 2009].

Some further discussions on various options for randomized studies appears in

Hedden S, Woolson R, Malcolm R. Randomization in substance abuse clinical trials. Substance Abuse Treatment, Prevention, and Policy. 2006;1(1):6. Available at: http://www.substanceabusepolicy.com/content/1/1/6 [Accessed February 18, 2009].

4. Monthly Mean Article: The challenges faced in the design, conduct and analysis of surgical RCTs

Cook J. The challenges faced in the design, conduct and analysis of surgical RCTs . Trials. 2009;10(1):9. Available at: http://www.trialsjournal.com/content/10/1/9 [Accessed February 10, 2009]. Description: Randomization is difficult in any study, but it is especially difficult in surgical trials. One issue is the timing of the randomization. You need to allow surgeons enough lead time to develop expertise with a new surgical trial, but during the time that this expertise is being developed, sufficient observational data may appear that would upset the balance of equipoise that is required by new trials. Furthermore, side effects and complications that do occur if randomization is done early may just reflect a lack of experience with a new type of surgery. Surgical trials also have difficulty attracting funding, compared to pharmaceutical interventions. There is a lot of money to be made marketing a new drug, and this potential for profit will attract a lot of investment money. Because surgical interventions cannot be bottled and shelved, there is no profit forces working to promote their use. Surgical trials, therefore, require a greater degree of government funding. Patient preferences may make randomization difficult when the comparison is between a surgical and non-surgical intervention. It is hard to find patients who are indifferent to surgery: either they want it really badly to get the problem fixed quickly, or they are scared of surgery and would prefer less invasive approaches. An added complication occurs because the doctor who performs the surgery is usually not the same doctor as the one who provides the non-surgical intervention. This adds heterogeneity to the process. Finally, blinding, a process that is relatively easy for many drug comparisons, is usually troublesome in surgical interventions. Unless the two surgical interventions are very similar, patients will usually know by the size and/or location of the scar which surgical technique was done. This article does suggest some recent innovations in clinical trial design that can help, but many of these issues will continue to cause problems for future randomized trials of surgical interventions.

5. Monthly Mean Blog: The Ask Edward Tufte Forum, Edward Tufte.

This is actually an RSS feed rather than a blog, but that's nitpicking. Edward Tufte is a prominent spokesperson for good graphic design. In this blog he takes reader questions and provides an answer and sometimes lets other reader chip in with their advice. There's a lot of interesting abstract discussion about aesthetic ideas, but also some very pragmatic advice. Some of the more interesting recent threads include

Election data displays

Excellent news graphics by Amanda Cox (NY Times)

Showing 3D measurement scales in 2D images (including astronomical pictures)

Advice for effective analytical reasoning

Lousy PowerPoint presentations: The fault of PP users?

6. Monthly Mean Book: How to report statistics in medicine, Lang TA, Secic M.

This is the perfect book for anyone who is uncertain of how to properly describe the statistical results in a research paper. There is a series of recommendations with sample wording ("When reporting percentages, always give the numerators and the denominators of the calculations"). Many sections include an example of how you would specifically word something ("Of 1000 men with heart disease, 800 (80%) had high serum cholesterol levels; of the 800, 250 (31%) were sedentary"). The advice is both sound and easy to follow. There are chapters on

Reporting numbers and descriptive statistics

Reporting measures of risk

Reporting estimates and confidence intervals.

Reporting hypothesis tests

The multiple testing problem

Reporting association and correlation analysis

Reporting regression analysis

Reporting analysis of variance (ANOVA)

Reporting survival analysis

Reporting the performance characteristics of diagnostic tests

Reporting Bayesian statistical analysis

Reporting Epidemiological Measures

Reporting randomized controlled trials

Reporting cohort or longitudinal studies

Reporting case-control studies

Reporting surveys or cross-sectional studies

Reporting systematic reviews and meta-analyses

Reporting economic evaluations

Reporting decision analyses and clinical practice guidelines

Reporting values, groups, and comparisons in tables

Reporting values, groups, and comparisons in figures

This is probably the book that I have recommended to people more than any other. There is a nice review of this book at http://ebm.bmj.com/cgi/content/full/12/3/90.

7. Monthly Mean Definition: What is a percentile?

The pth percentile of a data set is a value so that roughly p% of the data is smaller and (100-p)% of the data is larger. [[Note: the original newsletter had a typo here and incorrectly used the word "smaller" rather than "larger".]] Certainly commonly used percentiles have special names. The 50th percentile is commonly called the median. The quartiles of a data set represent the 25th, 50th, and 75th percentiles. The deciles of a data set represent the 10th, 20th, 30th, etc. percentiles. It should not be too hard to guess what the quintiles are. A bit more obscure are the tertiles, which are the values that split the data into three equal groups. Depending on what kind of nitpicker you are, the tertiles are the 33rd and 67th percentiles, maybe the 33.3 and 66.7 percentiles, or possibly even the 33 1/3 and 66 2/3 percentiles.

There several subtle issues in the definition of a percentile. First, some people insist that a percentile only makes sense if p is a whole number. These people would argue that there is a first percentile (1%) and a second percentile (2%) but not a 1.5 percentile. Second, if you express p as a proportion rather than a percent, then you need to use the term "quantile". Thus the 25th percentile and the 0.25 quantile are the same thing. But if you asked for the 0.25 percentile, you would either be out of order because 0.25 is not a whole number, or you would be asking for a value so that 0.25% (that is, 0.0025) of the data is smaller. I'm not as nitpicky as most people on this, but it always helps to use these terms precisely.

Often, researchers will define groups in terms of their percentiles. For example, in a study of ascorbic acid, the following result was noted in the abstract:

While diastolic blood pressure among persons in the lowest quartile of plasma ascorbic acid increased by 5.97 mmHg (95% CI 3.82 to 8.13 mmHg) from year 9 to year 10, those in the highest quartile of plasma vitamin C increased by only 0.23 mmHg (95% CI -1.90 to +2.36 mmHg)

Here the term "lowest quartile" means those patients whose plasma ascorbic acid was at or below the 25th percentile.

Finally, there is not a consensus in the research community on how to best calculate a percentile from a set of data. If your data set has 6 observations, there is no value that has exactly 25% of the data smaller than it. That's why I used the word "roughly" in my definition. A wikipedia article on percentiles offers a range of mathematical definitions. I prefer a simple definition. If you want to compute the pth percentile of a set of n values, compute p*(n+1)/100. If this value is a whole number choose that value from the data set ordered from smallest to largest. If it is a fractional value, round up and round down and choose the point halfway between the two rounded values. Thus for a set of 6 numbers, the 25th percentile is halfway between the first and second values in the ordered data set because p(n+1)/100 = 1.75. For a set of 7 numbers, the 25th percentile is the second value in the ordered data set because p(n+1)/100=2.

There are two nitpicky cases that still need to be mentioned with my formula. If p(n+1)/100 is less than 1, choose the smallest value and if it is greater than n, choose the largest value.

That seems messy, but some people advocate something even more complex. In the first situation listed above, where p(n+1)/100 is 1.75, they would not go halfway between the first and second number but rather 75% of the way towards the second number. So if the smallest value is 2 and the second smallest value is 6, make the 25th percentile 5 rather than 4. This is known linear interpolation. It might provide slightly better results, but life is too short to make all these extra calculations.

8. Monthly Mean Quote

If your experiment needs statistics, you ought to have done a better experiment. Ernest Rutherford, quoted at http://www.brainyquote.com/quotes/quotes/e/ernestruth391627.html. I disagree with this advice, of course, but it is too humorous not to mention.

9. Monthly Mean Website: Statistical Problems to Document and to Avoid, Frank Harrell

Most statisticians, including me, would benefit if we listened more carefully to the advice of Frank Harrell. He summarizes some important issues about statistical analysis in a checklist, Statistical Problems to Document and to Avoid. He mentions inefficiencies associated with categorizing continuous variables, inappropriate use of means and standard deviations for summarizing highly skewed data, failure to include confidence intervals, and problems associated with stepwise regression and overfitting. URL: http://biostat.mc.vanderbilt.edu/twiki/bin/view/Main/ManuscriptChecklist

10. Nick News: Nick the traveler, part 1.

Nicholas has always been a very good traveler. He was adopted from Russia, so as a two year old, he got to experience a lot more traveling than many adults. His first flight, from Kaliningrad to Moscow, went very smoothly.

Here's a picture of him on the airplane. He amused himself during the flight with an apple and a plastic knife and carved an elaborate apple structure.

Go to www.pmean.com/personal/traveler.html to see our favorite picture of the new family in front of St. Basil's cathedral and read about the long flight from Moscow to Kansas City.

11. Very bad joke: Face it-I'm your statistically significant other.

The comic xkcd is written by a true geek (and I use this word in a complimentary fashion). Someone on the EDSTAT-L internet mail discussion group noted the following comic, which is probably the first and only comic to include a boxplot.

I can include this comic strip directly in this newsletter, because the author (Randall Munroe) has a very liberal usage policy. I am very grateful to people on the web who make it easy to share their work. The main site for this comic strip is www.xkcd.com and the permanent link to this particular comic is http://xkcd.com/539/.

12. Tell me what you think.

How did you like this newsletter? I have three short open ended questions that I'd like to ask. It's totally optional on your part. Your responses will be kept anonymous, and will only be used to help improve future versions of this newsletter. You can also provide feedback by replying to this message. Unlike most newsletters where a reply goes into a black hole, a reply to this newsletter will go straight back to me.

January's newsletter produced three comments on the web survey and two emails.

Someone was nice enough to point out a broken link in the January newsletter. When I link to my own website, iContact gets confused, so I need to manually insert the proper URLs for these links. I forgot one, which was a plug for my book. The correct link is http://www.pmean.com/Evidence.html. The same person also pointed out that when adults fall, it's not only the greater mass, but also the greater velocity due to the fact that we are up higher than kids. Greater mass and greater velocity is a double whammy. Cathy's pretty much recovered from the skating experience, by the way.

I got a compliment for my section on crude versus adjusted comparisons. I was worried that it was a bit too technical. That person also wanted to see a discussion of generalized estimating equations in a future newsletter. I'm not sure I understand GEE models well enough to explain them clearly, but I will try to place them in the general context of repeated measures designs as a starting point. It may take a while for me to get something coherent written about this. This person also thought that "Nick News" was cute. Thanks!

Two people emphasized a desire for basic statistics, how-to tutorials, and general concepts. That's my general goal. I'm not writing for people who already know Statistics inside and out.

I also got a nice email from someone who liked my description of CART and the reference on overlapping confidence intervals. This person suggested some material on Bayesian models (more specifically, the Bayes factor). I had just come back from a conference on Bayesian Biostatistics, so the material is fresh in my mind. The hard part will be trying to make it accessible.

What now?

Sign up for the Monthly Mean newsletter

Review the archive of Monthly Mean newsletters

Go to the main page of the P.Mean website

Get help

This work is licensed under a Creative Commons Attribution 3.0 United States License. This page was written by Steve Simon and was last modified on 2017-06-15. Need more information? I have a page with general help resources. You can also browse for pages similar to this one at Category: Website details.